 login/create account
login/create account
Recent Activity
Convex uniform 5-polytopes ★★
Author(s):
Keywords:
MSO alternation hierarchy over pictures ★★
Author(s): Grandjean
Keywords: FMT12-LesHouches; MSO, alternation hierarchy; picture languages
Blatter-Specker Theorem for ternary relations ★★
Author(s): Makowsky
Let  be a class of finite relational structures. We denote by
be a class of finite relational structures. We denote by 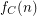 the number of structures in
the number of structures in  over the labeled set
over the labeled set 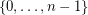 . For any class
. For any class  definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every
definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every 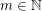 , the function
, the function 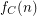 is ultimately periodic modulo
is ultimately periodic modulo  .
.
Keywords: Blatter-Specker Theorem; FMT00-Luminy
Monadic second-order logic with cardinality predicates ★★
Author(s): Courcelle
The problem concerns the extension of Monadic Second Order Logic (over a binary relation representing the edge relation) with the following atomic formulas:
- \item
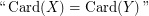 \item
\item 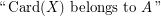
where  is a fixed recursive set of integers.
is a fixed recursive set of integers.
Let us fix  and a closed formula
and a closed formula 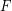 in this language.
in this language.
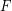 for a graph
for a graph  of tree-width at most
of tree-width at most  can be tested in polynomial time in the size of
can be tested in polynomial time in the size of  ?
? Keywords: bounded tree width; cardinality predicates; FMT03-Bedlewo; MSO
Order-invariant queries ★★
Author(s): Segoufin
- \item Does
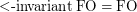 hold over graphs of bounded tree-width? \item Is
hold over graphs of bounded tree-width? \item Is 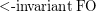 included in
included in 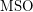 over graphs? \item Does
over graphs? \item Does 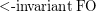 have a 0-1 law? \item Are properties of
have a 0-1 law? \item Are properties of 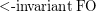 Hanf-local? \item Is there a logic (with an effective syntax) that captures
Hanf-local? \item Is there a logic (with an effective syntax) that captures 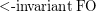 ?
? Keywords: Effective syntax; FMT12-LesHouches; Locality; MSO; Order invariance
Fixed-point logic with counting ★★
Author(s): Blass
- \item Given a graph, does it have a perfect matching, i.e., a set
 of edges such that every vertex is incident to exactly one edge from
of edges such that every vertex is incident to exactly one edge from  ? \item Given a square matrix over a finite field (regarded as a structure in the natural way, as described in [BGS02]), what is its determinant?
? \item Given a square matrix over a finite field (regarded as a structure in the natural way, as described in [BGS02]), what is its determinant? Keywords: Capturing PTime; counting quantifiers; Fixed-point logic; FMT03-Bedlewo
Birch & Swinnerton-Dyer conjecture ★★★★
Author(s):
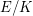 be an elliptic curve over a number field
be an elliptic curve over a number field 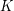 . Then the order of the zeros of its
. Then the order of the zeros of its 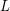 -function,
-function, 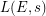 , at
, at 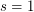 is the Mordell-Weil rank of
is the Mordell-Weil rank of 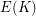 .
. Keywords:
Is Skewes' number e^e^e^79 an integer? ★★
Author(s):
Skewes' number 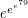 is not an integer.
is not an integer.
Keywords:
Minimal graphs with a prescribed number of spanning trees ★★
Author(s): Azarija; Skrekovski
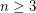 be an integer and let
be an integer and let 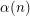 denote the least integer
denote the least integer  such that there exists a simple graph on
such that there exists a simple graph on  vertices having precisely
vertices having precisely  spanning trees. Then
spanning trees. Then 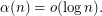
Keywords: number of spanning trees, asymptotics
Sticky Cantor sets ★★
Author(s):
 be a Cantor set embedded in
be a Cantor set embedded in 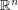 . Is there a self-homeomorphism
. Is there a self-homeomorphism  of
of 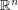 for every
for every  greater than
greater than  so that
so that  moves every point by less than
moves every point by less than  and
and 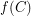 does not intersect
does not intersect  ? Such an embedded Cantor set for which no such
? Such an embedded Cantor set for which no such  exists (for some
exists (for some  ) is called "sticky". For what dimensions
) is called "sticky". For what dimensions  do sticky Cantor sets exist?
do sticky Cantor sets exist? Keywords: Cantor set
Subgroup formed by elements of order dividing n ★★
Author(s): Frobenius
Suppose  is a finite group, and
is a finite group, and  is a positive integer dividing
is a positive integer dividing 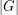 . Suppose that
. Suppose that  has exactly
has exactly  solutions to
solutions to 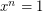 . Does it follow that these solutions form a subgroup of
. Does it follow that these solutions form a subgroup of  ?
?
Keywords: order, dividing
Giuga's Conjecture on Primality ★★
Author(s): Giuseppe Giuga
 is a prime iff
is a prime iff 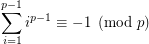
Keywords: primality
Coloring the Odd Distance Graph ★★★
Author(s): Rosenfeld
The Odd Distance Graph, denoted 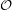 , is the graph with vertex set
, is the graph with vertex set 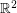 and two points adjacent if the distance between them is an odd integer.
and two points adjacent if the distance between them is an odd integer.
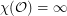 ?
? Keywords: coloring; geometric graph; odd distance
Cores of Cayley graphs ★★
Author(s): Samal
 be an abelian group. Is the core of a Cayley graph (on some power of
be an abelian group. Is the core of a Cayley graph (on some power of  ) a Cayley graph (on some power of
) a Cayley graph (on some power of  )?
)? Keywords: Cayley graph; core
Graph product of multifuncoids ★★
Author(s): Porton
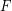 is a family of multifuncoids such that each
is a family of multifuncoids such that each 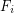 is of the form
is of the form 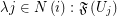 where
where 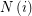 is an index set for every
is an index set for every 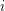 and
and 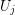 is a set for every
is a set for every 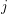 . Let every
. Let every 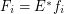 for some multifuncoid
for some multifuncoid 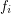 of the form
of the form 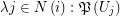 regarding the filtrator
regarding the filtrator 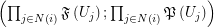 . Let
. Let  is a graph-composition of
is a graph-composition of 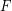 (regarding some partition
(regarding some partition  and external set
and external set 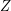 ). Then there exist a multifuncoid
). Then there exist a multifuncoid 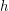 of the form
of the form 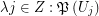 such that
such that 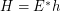 regarding the filtrator
regarding the filtrator 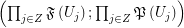 .
. Keywords: graph-product; multifuncoid
Atomicity of the poset of multifuncoids ★★
Author(s): Porton
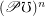 is for every sets
is for every sets 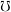 and
and  :
:- \item atomic; \item atomistic.
See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords: multifuncoid
Atomicity of the poset of completary multifuncoids ★★
Author(s): Porton
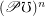 is for every sets
is for every sets 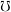 and
and  :
:- \item atomic; \item atomistic.
See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords: multifuncoid
Cycle double cover conjecture ★★★★
Upgrading a completary multifuncoid ★★
Author(s): Porton
Let 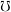 be a set,
be a set, 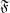 be the set of filters on
be the set of filters on 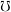 ordered reverse to set-theoretic inclusion,
ordered reverse to set-theoretic inclusion, 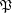 be the set of principal filters on
be the set of principal filters on 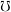 , let
, let  be an index set. Consider the filtrator
be an index set. Consider the filtrator 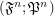 .
.
 is a completary multifuncoid of the form
is a completary multifuncoid of the form 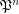 , then
, then 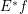 is a completary multifuncoid of the form
is a completary multifuncoid of the form 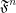 .
. See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords:

 and
and  are
are  Drupal
Drupal CSI of Charles University
CSI of Charles University