Open Problem Garden

In [MST02], Matz, Schweikardt, and Thomas, proved that the MSO-alternation hierarchy is strict over the class of 2-dimensional rectangular pictures (and, as a consequence, is also strict over the class of finite graphs).

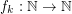The proof of this hierarchy strictness is essentially based on the fact that, for any positive integer , there is a function (defined as a fixed height tower of exponentials) such that the set of rectangular grids of format 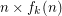(i.e, of width and length 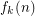) can be defined by some 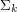MSO sentence but cannot be defined by some 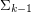MSO sentence.

So, the hierarchy result essentially rests on the (more than exponential) imbalance between the two dimensions of the rectangular grid.

In view of this result a natural question is as follows.

For example, for square picture languages (or equivalently, rectangular picture languages for which the width and the length of the pictures are linearly related), the only thing we know is that EMSO (that is Existential or 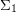MSO) over square pictures is not closed under complement.

Oliver Matz (personal communication) thinks it is possible that any MSO sentence over square pictures be equivalent to a Boolean combination of existntial MSO sentences.