 login/create account
login/create account
FMT12-LesHouches
Vertex Cover Integrality Gap ★★
Author(s): Atserias
Conjecture For every 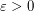 there is
there is 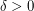 such that, for every large
such that, for every large  , there are
, there are  -vertex graphs
-vertex graphs  and
and  such that
such that 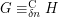 and
and 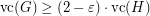 .
.
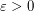 there is
there is 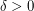 such that, for every large
such that, for every large  , there are
, there are  -vertex graphs
-vertex graphs  and
and  such that
such that 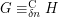 and
and 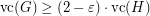 .
. Keywords: counting quantifiers; FMT12-LesHouches
Complexity of QBF(Bounded Treewidth) ★★
Author(s): Moshe Y. Vardi
Question What is the computational complexity of QBF(Bounded Treewidth)? Is it PSPACE-complete? In PTIME?
Keywords: bounded tree width; Computational Complexity; FMT12-LesHouches; QBF
MSO alternation hierarchy over pictures ★★
Author(s): Grandjean
Question Is the MSO-alternation hierarchy strict for pictures that are balanced, in the sense that the width and the length are polynomially (or linearly) related.
Keywords: FMT12-LesHouches; MSO, alternation hierarchy; picture languages
Order-invariant queries ★★
Author(s): Segoufin
Question
- \item Does
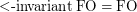 hold over graphs of bounded tree-width? \item Is
hold over graphs of bounded tree-width? \item Is 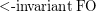 included in
included in 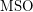 over graphs? \item Does
over graphs? \item Does 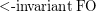 have a 0-1 law? \item Are properties of
have a 0-1 law? \item Are properties of 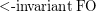 Hanf-local? \item Is there a logic (with an effective syntax) that captures
Hanf-local? \item Is there a logic (with an effective syntax) that captures 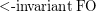 ?
? Keywords: Effective syntax; FMT12-LesHouches; Locality; MSO; Order invariance

 Drupal
Drupal CSI of Charles University
CSI of Charles University