 login/create account
login/create account
Vertex Cover Integrality Gap
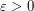 there is
there is 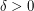 such that, for every large
such that, for every large  , there are
, there are  -vertex graphs
-vertex graphs  and
and  such that
such that 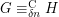 and
and 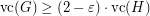 .
. Here 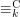 denotes indistinguishability in
denotes indistinguishability in  -variable first-order logic with counting quantifiers, and
-variable first-order logic with counting quantifiers, and 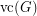 denotes the cardinality of the minimum vertex-cover of
denotes the cardinality of the minimum vertex-cover of  . By~[1],
. By~[1], 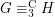 implies
implies 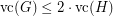 . Also by~[1] a positive answer would imply that an integrality gap of
. Also by~[1] a positive answer would imply that an integrality gap of 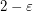 resists
resists 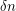 levels of Sherali-Adams linear programming relaxations of vertex-cover, on
levels of Sherali-Adams linear programming relaxations of vertex-cover, on  -vertex graphs. It is known that such a gap resists
-vertex graphs. It is known that such a gap resists 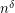 levels~[2]. What we ask would let us replace
levels~[2]. What we ask would let us replace 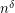 by
by 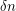 . If improving over
. If improving over 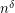 were not possible, then we could approximate vertex-cover by a factor better than~
were not possible, then we could approximate vertex-cover by a factor better than~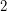 in subexponential time (i.e.
in subexponential time (i.e. 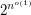 ). Approximating vertex-cover by a factor better than~1.36 is NP-hard~[3], and approximating vertex-cover by factor better than~2 is UG-hard~[4], where UG stands for Unique Games (from the Unique Games Conjecture); but note that UG-hardness does not rule out subexponential-time algorithms because UG itself is solvable in subexponential time~[5]
). Approximating vertex-cover by a factor better than~1.36 is NP-hard~[3], and approximating vertex-cover by factor better than~2 is UG-hard~[4], where UG stands for Unique Games (from the Unique Games Conjecture); but note that UG-hardness does not rule out subexponential-time algorithms because UG itself is solvable in subexponential time~[5]
Bibliography
[1] A. Atserias and E. Maneva. Sherali-Adams Relaxations and Indistinguishability in Counting Logics, in Proc. 3rd ACM ITCS, pp. 367-379, 2012.
[2] M. Charikar, K. Makarychev and Y. Makarychev. Integrality Gaps for Sherali-Adams Relaxations, in Proc. 41st ACM STOC, pp. 283-292, 2009.
[3] I. Dinur and S. Safra. On the Hardness of Approximating Minimum Vertex-Cover, Annals of Mathematics, 162(1):439-485, 2005.
[4] S. Khot and O. Regev. Vertex cover might be hard to approximate to within 2-epsilon, J. Comput. Syst. Sci. 74(3):335-349, 2008.
[5] S. Arora, B. Barak, and D. Steurer. Subexponential Algorithms for Unique Games and Related problems, in Proc. 51th IEEE FOCS, pp. 563-572, 2010.}
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University