Open Problem Garden

Importance: Medium ✭✭

Author(s):

Subject:	Logic
	» Finite Model Theory

Keywords:	counting quantifiers
	FMT12-LesHouches

Recomm. for undergrads: no

Posted	by:	dberwanger
	on:	October 2nd, 2012

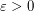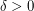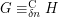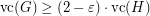Conjecture For every $\varepsilon > 0$ there is $\delta > 0$ such that, for every large $n$ , there are $n$ -vertex graphs $G$ and $H$ such that $G \equiv_{\delta n}^{\mathrm{C}} H$ and $\mathrm{vc}(G) \ge (2 - \varepsilon) \cdot \mathrm{vc}(H)$ .

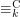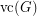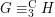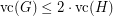Here $\equiv^{\mathrm{C}}_{k}$ denotes indistinguishability in $k$ -variable first-order logic with counting quantifiers, and $\mathrm{vc}(G)$ denotes the cardinality of the minimum vertex-cover of $G$ . By~[1], $G \equiv_{3}^{\mathrm{C}} H$ implies $\mathrm{vc}(G) \leq 2 \cdot \mathrm{vc}(H)$ . Also by~[1] a positive answer would imply that an integrality gap of 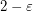$2-\varepsilon$ resists 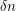$\delta n$ levels of Sherali-Adams linear programming relaxations of vertex-cover, on $n$ -vertex graphs. 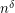It is known that such a gap resists $n^{\delta}$ levels~[2]. 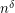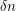What we ask would let us replace $n^{\delta}$ by $\delta n$ . If improving over 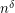$n^{\delta}$ were not possible, then we could approximate vertex-cover by a factor better than~ $2$ in subexponential time (i.e. $2^{n^{o(1)}}$ ). 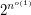Approximating vertex-cover by a factor better than~1.36 is NP-hard~[3], and approximating vertex-cover by factor better than~2 is UG-hard~[4], where UG stands for Unique Games (from the Unique Games Conjecture); but note that UG-hardness does not rule out subexponential-time algorithms because UG itself is solvable in subexponential time~[5]

Bibliography

[1] A. Atserias and E. Maneva. Sherali-Adams Relaxations and Indistinguishability in Counting Logics, in Proc. 3rd ACM ITCS, pp. 367-379, 2012.

[2] M. Charikar, K. Makarychev and Y. Makarychev. Integrality Gaps for Sherali-Adams Relaxations, in Proc. 41st ACM STOC, pp. 283-292, 2009.

[3] I. Dinur and S. Safra. On the Hardness of Approximating Minimum Vertex-Cover, Annals of Mathematics, 162(1):439-485, 2005.

[4] S. Khot and O. Regev. Vertex cover might be hard to approximate to within 2-epsilon, J. Comput. Syst. Sci. 74(3):335-349, 2008.

[5] S. Arora, B. Barak, and D. Steurer. Subexponential Algorithms for Unique Games and Related problems, in Proc. 51th IEEE FOCS, pp. 563-572, 2010.}

* indicates original appearance(s) of problem.

add new comment

Open Problem Garden

Bibliography

Reply

Navigate

Recent Activity