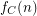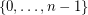Let be a class of finite relational structures. We denote by the number of structures in over the labeled set . For any class definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every 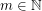, the function 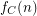is ultimately periodic modulo .