 login/create account
login/create account
Let  be a class of finite relational structures. We denote by
be a class of finite relational structures. We denote by 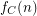 the number of structures in
the number of structures in  over the labeled set
over the labeled set 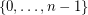 . For any class
. For any class  definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every
definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every 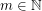 , the function
, the function 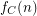 is ultimately periodic modulo
is ultimately periodic modulo  .
.
Our exposition follows closely [BS84].
Counting labeled structures modulo 
Let  be a class of finite structures for one binary relation symbol
be a class of finite structures for one binary relation symbol 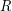 . We define for
. We define for 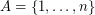
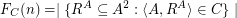
Examples:
- \item If
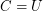 consists of all
consists of all 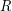 -structures,
-structures, 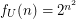 . \item If
. \item If 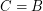 consists of bijections,
consists of bijections, 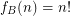 \item If
\item If 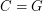 is the class of all (undirected, simple) graphs,
is the class of all (undirected, simple) graphs, 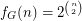 . \item If
. \item If 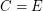 is the class of all equivalence relations, then
is the class of all equivalence relations, then 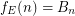 , the {\em Bell Numbers}. \item If
, the {\em Bell Numbers}. \item If 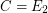 is the class of all equivalence relations with two classes only, of the same size,
is the class of all equivalence relations with two classes only, of the same size, 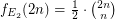 . Clearly,
. Clearly, 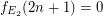 . \item If
. \item If 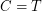 is the class of all trees,
is the class of all trees, 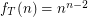 , {\em Caley}.
, {\em Caley}. We observe the following:
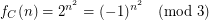
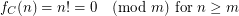
And for each  the functions,
the functions, 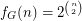 ,
, 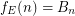 ,
, 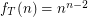 are ultimately periodic
are ultimately periodic 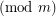 .
.
However, 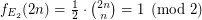 iff
iff 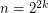 , hence is not periodic
, hence is not periodic 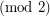 .
.
Monadic second-order logic definable classes
The first four examples (all relations, all bijections, all graphs, all equivalence relations) are definable in First Order Logic 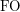 . The trees are definable in Monadic Second Order Logic
. The trees are definable in Monadic Second Order Logic 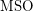 ..
..
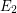 is definable in Second Order Logic
is definable in Second Order Logic 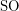 , but it is not
, but it is not 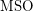 -definable. If we expand
-definable. If we expand 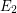 to have the bijection between the classes we get structures with two binary relations. The class is now
to have the bijection between the classes we get structures with two binary relations. The class is now 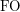 -definable. Let us denote the corresponding counting function
-definable. Let us denote the corresponding counting function 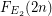 . We have
. We have 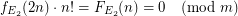 for
for  large enough.
large enough.
Periodicity and linear recurrence relations
The periodicity of 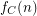
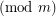 is usually established by exhibiting a linear recurrence relation:
is usually established by exhibiting a linear recurrence relation:
There exists 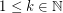 and integers
and integers 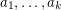 such that for all
such that for all 
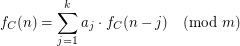
Examples.
- \item In the case of
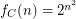 we have
we have 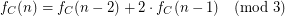 \item In the case of
\item In the case of 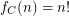 we have for all
we have for all 
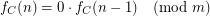 In this case we say that
In this case we say that 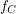 trivializes.
trivializes. The Blatter-Specker Theorem
 be a binary vocabulary, i.e. all relation symbols are at most binary. If
be a binary vocabulary, i.e. all relation symbols are at most binary. If  is a class of finite
is a class of finite  -structures which is
-structures which is  -definable, then for all
-definable, then for all 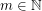
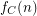 is ultimately periodic
is ultimately periodic 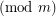 .
.
Moreover, there exists 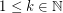 and integers
and integers 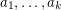 such that for all
such that for all 
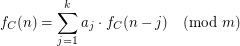 i.e we have a linear recurrence relation.
i.e we have a linear recurrence relation.
In [F03] Fischer showed that the Specker-Blatter Theorem does not hold for quaternary relations.
The case of ternary relations remains open.
See also [FM06] for further developments on the topic.
Bibliography
[BS84]* C. Blatter and E. Specker, Recurrence relations for the number of labeled structures on a finite set, Logic and Machines: Decision Problems and Complexity, E. Börger, G. Hasenjaeger and D. Rödding, eds, LNCS 171 (1984) pp. 43-61.
[F03] E. Fischer, The Specker-Blatter theorem does not hold for quaternary relations, Journal of Combinatorial Theory Series A 103(2003), 121-136.
[FM06] E. Fischer and J. A. Makowsky, The Specker-Blatter Theorem revisited: Generating functions for definable classes of stuctures. In Computing and Combinatorics (COCOON 2003) Proc., LNCS vol. 2697 (2003), 90-101.
[S88] E. Specker, Application of Logic and Combinatorics to Enumeration Problems, Trends in Theoretical Computer Science, E. Börger ed., Computer Science Press, 1988, pp. 141-169. Reprinted in: Ernst Specker, Selecta, Birkhäuser 1990, pp. 324-350.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University