 login/create account
login/create account
Samal, Robert
Star chromatic index of complete graphs ★★
Author(s): Dvorak; Mohar; Samal
Conjecture Is it possible to color edges of the complete graph  using
using 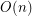 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
 using
using 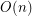 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
Equivalently: is the star chromatic index of  linear in
linear in  ?
?
Keywords: complete graph; edge coloring; star coloring
Star chromatic index of cubic graphs ★★
Author(s): Dvorak; Mohar; Samal
The star chromatic index 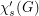 of a graph
of a graph  is the minimum number of colors needed to properly color the edges of the graph so that no path or cycle of length four is bi-colored.
is the minimum number of colors needed to properly color the edges of the graph so that no path or cycle of length four is bi-colored.
Question Is it true that for every (sub)cubic graph  , we have
, we have 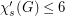 ?
?
 , we have
, we have 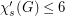 ?
? Keywords: edge coloring; star coloring
Weak pentagon problem ★★
Author(s): Samal
Conjecture If  is a cubic graph not containing a triangle, then it is possible to color the edges of
is a cubic graph not containing a triangle, then it is possible to color the edges of  by five colors, so that the complement of every color class is a bipartite graph.
by five colors, so that the complement of every color class is a bipartite graph.
 is a cubic graph not containing a triangle, then it is possible to color the edges of
is a cubic graph not containing a triangle, then it is possible to color the edges of  by five colors, so that the complement of every color class is a bipartite graph.
by five colors, so that the complement of every color class is a bipartite graph. Keywords: Clebsch graph; cut-continuous mapping; edge-coloring; homomorphism; pentagon
Drawing disconnected graphs on surfaces ★★
Author(s): DeVos; Mohar; Samal
Conjecture Let  be the disjoint union of the graphs
be the disjoint union of the graphs  and
and  and let
and let 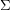 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on 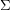 has the property that
has the property that  and
and  are disjoint?
are disjoint?
 be the disjoint union of the graphs
be the disjoint union of the graphs  and
and  and let
and let 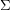 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on 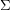 has the property that
has the property that  and
and  are disjoint?
are disjoint? Keywords: crossing number; surface
Cores of Cayley graphs ★★
Author(s): Samal
Conjecture Let  be an abelian group. Is the core of a Cayley graph (on some power of
be an abelian group. Is the core of a Cayley graph (on some power of  ) a Cayley graph (on some power of
) a Cayley graph (on some power of  )?
)?
 be an abelian group. Is the core of a Cayley graph (on some power of
be an abelian group. Is the core of a Cayley graph (on some power of  ) a Cayley graph (on some power of
) a Cayley graph (on some power of  )?
)? Keywords: Cayley graph; core

 Drupal
Drupal CSI of Charles University
CSI of Charles University