 login/create account
login/create account
Star chromatic index of complete graphs
Conjecture Is it possible to color edges of the complete graph  using
using 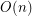 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
 using
using 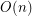 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
Equivalently: is the star chromatic index of  linear in
linear in  ?
?
The star chromatic index 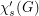 of a graph
of a graph  is the minimum number of colors needed to properly color the edges of
is the minimum number of colors needed to properly color the edges of  so that no path or cycle of length four is bi-colored. An equivalent definition is that
so that no path or cycle of length four is bi-colored. An equivalent definition is that 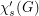 is the star chromatic number of the line graph
is the star chromatic number of the line graph 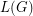 .
.
Dvořák, Mohar, and Šámal [DMS] show that 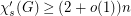 . On the other hand, the best known upper bound (also in \cite{DMS]) is superlinear:
. On the other hand, the best known upper bound (also in \cite{DMS]) is superlinear: 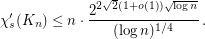
It may be possible to decrease the upper bound by elementary methods.
Bibliography
*[DMS] Dvořák, Zdeněk; Mohar, Bojan; Šámal, Robert: Star chromatic index, arXiv:1011.3376.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University