 login/create account
login/create account
edge coloring
Star chromatic index of complete graphs ★★
Author(s): Dvorak; Mohar; Samal
Conjecture Is it possible to color edges of the complete graph 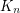 using
using 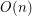 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
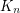 using
using 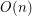 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
Equivalently: is the star chromatic index of 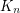 linear in
linear in  ?
?
Keywords: complete graph; edge coloring; star coloring
Star chromatic index of cubic graphs ★★
Author(s): Dvorak; Mohar; Samal
The star chromatic index 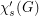 of a graph
of a graph  is the minimum number of colors needed to properly color the edges of the graph so that no path or cycle of length four is bi-colored.
is the minimum number of colors needed to properly color the edges of the graph so that no path or cycle of length four is bi-colored.
Question Is it true that for every (sub)cubic graph  , we have
, we have 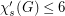 ?
?
 , we have
, we have 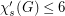 ?
? Keywords: edge coloring; star coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University