 login/create account
login/create account
edge-coloring
Edge-antipodal colorings of cubes ★★
Author(s): Norine
We let 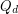 denote the
denote the  -dimensional cube graph. A map
-dimensional cube graph. A map 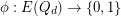 is called edge-antipodal if
is called edge-antipodal if 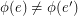 whenever
whenever 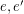 are antipodal edges.
are antipodal edges.
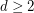 and
and 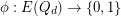 is edge-antipodal, then there exist a pair of antipodal vertices
is edge-antipodal, then there exist a pair of antipodal vertices 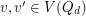 which are joined by a monochromatic path.
which are joined by a monochromatic path. Keywords: antipodal; cube; edge-coloring
Goldberg's conjecture ★★★
Author(s): Goldberg
The overfull parameter is defined as follows: ![\[ w(G) = \max_{H \subseteq G} \left\lceil \frac{ |E(H)| }{ \lfloor \tfrac{1}{2} |V(H)| \rfloor} \right\rceil. \]](/files/tex/d2391343543ce03d861e6eb2f4985d52e309525d.png)
 satisfies
satisfies 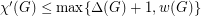 .
. Keywords: edge-coloring; multigraph
Seymour's r-graph conjecture ★★★
Author(s): Seymour
An  -graph is an
-graph is an  -regular graph
-regular graph  with the property that
with the property that 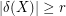 for every
for every 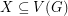 with odd size.
with odd size.
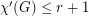 for every
for every  -graph
-graph  .
. Keywords: edge-coloring; r-graph
Monochromatic reachability or rainbow triangles ★★★
Author(s): Sands; Sauer; Woodrow
In an edge-colored digraph, we say that a subgraph is rainbow if all its edges have distinct colors, and monochromatic if all its edges have the same color.
 be a tournament with edges colored from a set of three colors. Is it true that
be a tournament with edges colored from a set of three colors. Is it true that  must have either a rainbow directed cycle of length three or a vertex
must have either a rainbow directed cycle of length three or a vertex  so that every other vertex can be reached from
so that every other vertex can be reached from  by a monochromatic (directed) path?
by a monochromatic (directed) path? Keywords: digraph; edge-coloring; tournament
Monochromatic reachability in edge-colored tournaments ★★★
Author(s): Erdos
 , is there a (least) positive integer
, is there a (least) positive integer 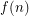 so that whenever a tournament has its edges colored with
so that whenever a tournament has its edges colored with  colors, there exists a set
colors, there exists a set  of at most
of at most 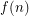 vertices so that every vertex has a monochromatic path to some point in
vertices so that every vertex has a monochromatic path to some point in  ?
? Keywords: digraph; edge-coloring; tournament
Weak pentagon problem ★★
Author(s): Samal
 is a cubic graph not containing a triangle, then it is possible to color the edges of
is a cubic graph not containing a triangle, then it is possible to color the edges of  by five colors, so that the complement of every color class is a bipartite graph.
by five colors, so that the complement of every color class is a bipartite graph. Keywords: Clebsch graph; cut-continuous mapping; edge-coloring; homomorphism; pentagon
List colorings of edge-critical graphs ★★
Author(s): Mohar
 is a
is a 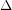 -edge-critical graph. Suppose that for each edge
-edge-critical graph. Suppose that for each edge  of
of  , there is a list
, there is a list 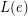 of
of 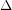 colors. Then
colors. Then  is
is 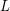 -edge-colorable unless all lists are equal to each other.
-edge-colorable unless all lists are equal to each other. Keywords: edge-coloring; list coloring
A generalization of Vizing's Theorem? ★★
Author(s): Rosenfeld
 be a simple
be a simple  -uniform hypergraph, and assume that every set of
-uniform hypergraph, and assume that every set of 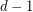 points is contained in at most
points is contained in at most  edges. Then there exists an
edges. Then there exists an 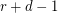 -edge-coloring so that any two edges which share
-edge-coloring so that any two edges which share 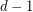 vertices have distinct colors.
vertices have distinct colors. Keywords: edge-coloring; hypergraph; Vizing
Partitioning edge-connectivity ★★
Author(s): DeVos
 be an
be an 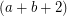 -edge-connected graph. Does there exist a partition
-edge-connected graph. Does there exist a partition 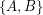 of
of 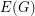 so that
so that 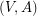 is
is  -edge-connected and
-edge-connected and 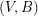 is
is  -edge-connected?
-edge-connected? Keywords: edge-coloring; edge-connectivity
Acyclic edge-colouring ★★
Author(s): Fiamcik
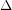 has a proper
has a proper 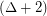 -edge-colouring so that every cycle contains edges of at least three distinct colours.
-edge-colouring so that every cycle contains edges of at least three distinct colours. Keywords: edge-coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University