 login/create account
login/create account
Goldberg's conjecture
The overfull parameter is defined as follows: ![\[ w(G) = \max_{H \subseteq G} \left\lceil \frac{ |E(H)| }{ \lfloor \tfrac{1}{2} |V(H)| \rfloor} \right\rceil. \]](/files/tex/d2391343543ce03d861e6eb2f4985d52e309525d.png)
 satisfies
satisfies 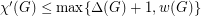 .
. This important problem remains open despite considerable attention. The same conjecture was independently discovered by Andersen and Seymour.
Vizing's Theorem, one of the cornerstones of graph colouring, shows that 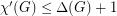 for every simple graph
for every simple graph  . So, in particular, every simple graph satisfies Goldberg's conjecture. Graphs with parallel edges need not satisfy Vizing's bound. For instance, if
. So, in particular, every simple graph satisfies Goldberg's conjecture. Graphs with parallel edges need not satisfy Vizing's bound. For instance, if  is the graph obtained from a triangle by adding an extra
is the graph obtained from a triangle by adding an extra  edges in parallel with each existing one, then
edges in parallel with each existing one, then 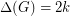 but
but 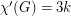 . More generally, if
. More generally, if  is a subgraph of
is a subgraph of  , then every colour can appear on at most
, then every colour can appear on at most 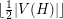 edges of
edges of  , so
, so 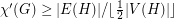 . Thus,
. Thus, 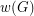 , our overfull parameter, is a natural lower bound on
, our overfull parameter, is a natural lower bound on 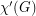 , and Goldberg's conjecture asserts that whenever
, and Goldberg's conjecture asserts that whenever 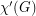 exceeds
exceeds 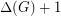 , then it is equal to this lower bound.
, then it is equal to this lower bound.
Although the statement of the conjecture may appear to be the most natural formulation, there are a couple of related conjectures with similar lower bounds. For instance, Seymour's r-graph conjecture is equivalent to the statement that 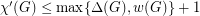 . Goldberg also conjectured that
. Goldberg also conjectured that 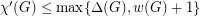 .
.
In addition to simple graphs, Goldberg's Conjecture is known to hold for any graph  which satisfies one of the following
which satisfies one of the following
- \item
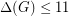 \item
\item  has no minor isomorphic to
has no minor isomorphic to 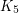 minus an edge. \item
minus an edge. \item 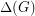 is sufficiently large in comparison with
is sufficiently large in comparison with 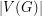 .
. 
Packers And Movers Chandigarh
Packers And Movers Hyderabad
Packers And Movers Bangalore
Bibliography
*[G] M. K. Goldberg, Multigraphs with a chromatic index that is nearly maximal. (Russian) A collection of articles dedicated to the memory of Vitaliĭ Konstantinovič Korobkov. Diskret. Analiz No. 23 (1973), 3--7, 72. MathSciNet
* indicates original appearance(s) of problem.
Different Goldberg Conjecture?
http://plms.oxfordjournals.org/content/106/4/703
--Stephen

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Latest Developments
Stiebitz et al(2006), Yu(2008) and Kurt(2009) has separately shown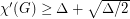 implies Goldberg Conjecture. While Yu's method gives a methodological approach to the general problem, Kurt provides a very short and elementary proof.
implies Goldberg Conjecture. While Yu's method gives a methodological approach to the general problem, Kurt provides a very short and elementary proof.
Scheide (2008) has shown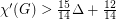 implies the Goldberg Conjecture.
implies the Goldberg Conjecture.
Kurt(2009) has shown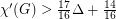 implies the Goldberg Conjecture.
implies the Goldberg Conjecture.