 login/create account
login/create account
Nowhere-zero flows
Open problems about Nowhere-zero flows (not to be confused with Network flows).
5-flow conjecture ★★★★
Author(s): Tutte
Keywords: cubic; nowhere-zero flow
3-flow conjecture ★★★
Author(s): Tutte
Keywords: nowhere-zero flow
Jaeger's modular orientation conjecture ★★★
Author(s): Jaeger
Keywords: nowhere-zero flow; orientation
Bouchet's 6-flow conjecture ★★★
Author(s): Bouchet
 -flow for some
-flow for some  , has a nowhere-zero
, has a nowhere-zero  -flow.
-flow. Keywords: bidirected graph; nowhere-zero flow
The three 4-flows conjecture ★★
Author(s): DeVos
 with no bridge, there exist three disjoint sets
with no bridge, there exist three disjoint sets 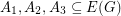 with
with 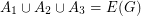 so that
so that 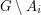 has a nowhere-zero 4-flow for
has a nowhere-zero 4-flow for 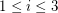 .
. Keywords: nowhere-zero flow
A homomorphism problem for flows ★★
Author(s): DeVos
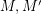 be abelian groups and let
be abelian groups and let 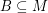 and
and 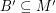 satisfy
satisfy 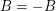 and
and 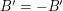 . If there is a homomorphism from
. If there is a homomorphism from 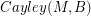 to
to 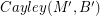 , then every graph with a B-flow has a B'-flow.
, then every graph with a B-flow has a B'-flow. Keywords: homomorphism; nowhere-zero flow; tension
Real roots of the flow polynomial ★★
Author(s): Welsh
Keywords: flow polynomial; nowhere-zero flow
Unit vector flows ★★
Author(s): Jain
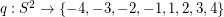 so that antipodal points of
so that antipodal points of 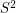 receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero.
receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero. Keywords: nowhere-zero flow
Antichains in the cycle continuous order ★★
Author(s): DeVos
If  ,
, are graphs, a function
are graphs, a function 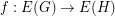 is called cycle-continuous if the pre-image of every element of the (binary) cycle space of
is called cycle-continuous if the pre-image of every element of the (binary) cycle space of  is a member of the cycle space of
is a member of the cycle space of  .
.
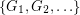 so that there is no cycle continuous mapping between
so that there is no cycle continuous mapping between 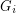 and
and 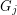 whenever
whenever 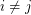 ?
? Circular flow number of regular class 1 graphs ★★
Author(s): Steffen
A nowhere-zero  -flow
-flow 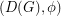 on
on  is an orientation
is an orientation  of
of  together with a function
together with a function 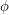 from the edge set of
from the edge set of  into the real numbers such that
into the real numbers such that 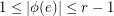 , for all
, for all 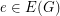 , and
, and 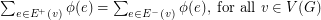 . The circular flow number of
. The circular flow number of  is inf
is inf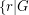 has a nowhere-zero
has a nowhere-zero  -flow
-flow 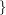 , and it is denoted by
, and it is denoted by 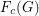 .
.
A graph with maximum vertex degree  is a class 1 graph if its edge chromatic number is
is a class 1 graph if its edge chromatic number is  .
.
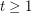 be an integer and
be an integer and  a
a 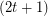 -regular graph. If
-regular graph. If  is a class 1 graph, then
is a class 1 graph, then 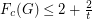 .
. 
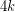 -
-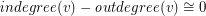 (mod
(mod 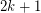 ) for every vertex
) for every vertex  .
. 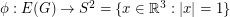 .
.
 Drupal
Drupal CSI of Charles University
CSI of Charles University