 login/create account
login/create account
poset
Antichains in the cycle continuous order ★★
Author(s): DeVos
If  ,
, are graphs, a function
are graphs, a function 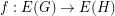 is called cycle-continuous if the pre-image of every element of the (binary) cycle space of
is called cycle-continuous if the pre-image of every element of the (binary) cycle space of  is a member of the cycle space of
is a member of the cycle space of  .
.
Problem Does there exist an infinite set of graphs 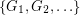 so that there is no cycle continuous mapping between
so that there is no cycle continuous mapping between 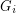 and
and 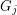 whenever
whenever 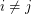 ?
?
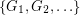 so that there is no cycle continuous mapping between
so that there is no cycle continuous mapping between 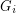 and
and 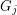 whenever
whenever 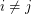 ?
? 
 Drupal
Drupal CSI of Charles University
CSI of Charles University