 login/create account
login/create account
Circular flow number of regular class 1 graphs
A nowhere-zero  -flow
-flow 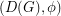 on
on  is an orientation
is an orientation  of
of  together with a function
together with a function 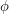 from the edge set of
from the edge set of  into the real numbers such that
into the real numbers such that 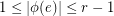 , for all
, for all 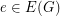 , and
, and 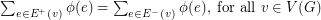 . The circular flow number of
. The circular flow number of  is inf
is inf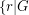 has a nowhere-zero
has a nowhere-zero  -flow
-flow 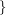 , and it is denoted by
, and it is denoted by 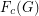 .
.
A graph with maximum vertex degree  is a class 1 graph if its edge chromatic number is
is a class 1 graph if its edge chromatic number is  .
.
Conjecture Let 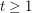 be an integer and
be an integer and  a
a 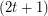 -regular graph. If
-regular graph. If  is a class 1 graph, then
is a class 1 graph, then 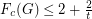 .
.
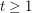 be an integer and
be an integer and  a
a 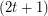 -regular graph. If
-regular graph. If  is a class 1 graph, then
is a class 1 graph, then 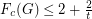 .
.
The conjecture is true for 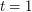 , i.e. for cubic graphs. It says, that the circular flow number of
, i.e. for cubic graphs. It says, that the circular flow number of 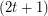 -regular class 1 graphs is bounded by the circular flow number of the complete graph on
-regular class 1 graphs is bounded by the circular flow number of the complete graph on 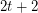 vertices.
vertices.
Bibliography
[ES_2001] E. Steffen, Circular flow numbers of regular multigraphs, J. Graph Theory 36, 24 – 34 (2001)
*[ES_2015] E. Steffen, Edge-colorings and circular flow numbers on regular graphs, J. Graph Theory 79, 1–7, 2015
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University