 login/create account
login/create account
Jaeger called an orientation with the above property a modular 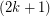 -orientation, and observed that a graph has a modular
-orientation, and observed that a graph has a modular 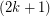 -orientation if and only if it has a
-orientation if and only if it has a 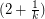 -flow. Thus, this conjecture may be seen as a sharp form of the 2+epsilon flow conjecture. For k=1, this problem is precisely the 3-flow conjecture, and for k=2, Jaeger showed that this conjecture (if true) would imply the 5-flow conjecture. If true, this conjecture would be best possible for every value of k.
-flow. Thus, this conjecture may be seen as a sharp form of the 2+epsilon flow conjecture. For k=1, this problem is precisely the 3-flow conjecture, and for k=2, Jaeger showed that this conjecture (if true) would imply the 5-flow conjecture. If true, this conjecture would be best possible for every value of k.
The restriction of this conjecture to planar graphs is open, and has a dual formulation. See Mapping planar graphs to odd cycles.
Bibliography
[J] F. Jaeger, On circular flows in graphs. Finite and infinite sets, Vol. I, II (Eger, 1981), 391--402, Colloq. Math. Soc. János Bolyai, 37, North-Holland, Amsterdam, 1984.. MathSciNet
* indicates original appearance(s) of problem.

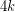 -
-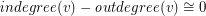 (mod
(mod 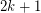 ) for every vertex
) for every vertex  .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University