 login/create account
login/create account
(2 + epsilon)-flow conjecture (Solved)
Definition: If  is a directed graph and
is a directed graph and 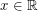 , a real
, a real  -flow (sometimes abbreviated
-flow (sometimes abbreviated  -flow) of
-flow) of  is a real valued flow
is a real valued flow 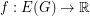 with the property that
with the property that 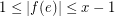 for every
for every 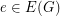 . As in the case of nowhere-zero flows, the existence of an
. As in the case of nowhere-zero flows, the existence of an  -flow in a graph does not depend on the orientation, and we say that an undirected graph has an
-flow in a graph does not depend on the orientation, and we say that an undirected graph has an  -flow if some (and thus every) orientation of it admits such a flow. It is a simple exercise to prove that every graph with a real
-flow if some (and thus every) orientation of it admits such a flow. It is a simple exercise to prove that every graph with a real  -flow has an (integer) nowhere-zero
-flow has an (integer) nowhere-zero  -flow where
-flow where 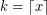 . Thus, we may view
. Thus, we may view  -flows as a refinement of nowhere-zero
-flows as a refinement of nowhere-zero  -flows.
-flows.
This conjecture has a strong intuitive appeal. Simply put, the above conjecture asserts that in a graph with high edge-connectivity, it is possible to find a real-valued flow where every edge has about the same flow value. By the above comment relating  -flows and nowhere-zero
-flows and nowhere-zero  -flows, this conjecture (if true) would imply The weak 3-flow conjecture (See 3-flow conjecture). Zhang [Z] has proved that this result holds when restricted to graphs on a fixed surface, but little else seems to be known.
-flows, this conjecture (if true) would imply The weak 3-flow conjecture (See 3-flow conjecture). Zhang [Z] has proved that this result holds when restricted to graphs on a fixed surface, but little else seems to be known.
L. M. Lovász, C. Thomassen, Y. Wu, and C.-Q. Zhang solved this conjecture by proving the following.
For every positive integer  , every
, every 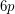 -edge-conneected graph admits a nowhere-zero circular
-edge-conneected graph admits a nowhere-zero circular 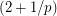 -flow.
-flow.
Bibliography
[KZ] W. Klostermeyer and C. Q. Zhang, 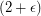 -coloring of planar graphs with large odd-girth. Graph Theory 33 (2000), no. 2, 109--119. MathSciNet
-coloring of planar graphs with large odd-girth. Graph Theory 33 (2000), no. 2, 109--119. MathSciNet
[Z] C. Q. Zhang, Cun Quan, Circular flows of nearly Eulerian graphs and vertex-splitting. J. Graph Theory 40 (2002), no. 3, 147--161. MathSciNet
[LTWZ] L. M. Lovász, C. Thomassen, Y. Wu, and C.-Q. Zhang. Nowhere-zero 3-flows and modulo k-orientations. J. Combin. Theory Ser. B, 103(5):587–598, 2013.
* indicates original appearance(s) of problem.

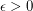 there exists an integer
there exists an integer  Drupal
Drupal CSI of Charles University
CSI of Charles University
$ (2+\epsilon) $-flow conjecture.
The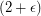 -flow conjecture is a consequence of the weak circular flow conjecture which was proved in
-flow conjecture is a consequence of the weak circular flow conjecture which was proved in
[T] C.Thomassen, The weak 3-flow conjecture and the weak circular flow conjecture, J.Combinatorial Theory B 102 (2012) 521-529.
The paper [LTWZ] gives an improved bound.