 login/create account
login/create account
digraph
Monochromatic reachability or rainbow triangles ★★★
Author(s): Sands; Sauer; Woodrow
In an edge-colored digraph, we say that a subgraph is rainbow if all its edges have distinct colors, and monochromatic if all its edges have the same color.
 be a tournament with edges colored from a set of three colors. Is it true that
be a tournament with edges colored from a set of three colors. Is it true that  must have either a rainbow directed cycle of length three or a vertex
must have either a rainbow directed cycle of length three or a vertex  so that every other vertex can be reached from
so that every other vertex can be reached from  by a monochromatic (directed) path?
by a monochromatic (directed) path? Keywords: digraph; edge-coloring; tournament
Monochromatic reachability in edge-colored tournaments ★★★
Author(s): Erdos
 , is there a (least) positive integer
, is there a (least) positive integer 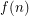 so that whenever a tournament has its edges colored with
so that whenever a tournament has its edges colored with  colors, there exists a set
colors, there exists a set  of at most
of at most 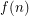 vertices so that every vertex has a monochromatic path to some point in
vertices so that every vertex has a monochromatic path to some point in  ?
? Keywords: digraph; edge-coloring; tournament
Non-edges vs. feedback edge sets in digraphs ★★★
Author(s): Chudnovsky; Seymour; Sullivan
For any simple digraph  , we let
, we let 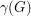 be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and
be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and 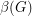 be the size of the smallest feedback edge set.
be the size of the smallest feedback edge set.
 is a simple digraph without directed cycles of length
is a simple digraph without directed cycles of length 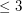 , then
, then 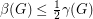 .
. Keywords: acyclic; digraph; feedback edge set; triangle free
Highly arc transitive two ended digraphs ★★
Author(s): Cameron; Praeger; Wormald
 is a highly arc transitive digraph with two ends, then every tile of
is a highly arc transitive digraph with two ends, then every tile of  is a disjoint union of complete bipartite graphs.
is a disjoint union of complete bipartite graphs. Keywords: arc transitive; digraph; infinite graph
Universal highly arc transitive digraphs ★★★
Author(s): Cameron; Praeger; Wormald
An alternating walk in a digraph is a walk 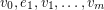 so that the vertex
so that the vertex 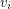 is either the head of both
is either the head of both 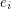 and
and 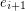 or the tail of both
or the tail of both 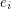 and
and 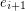 for every
for every 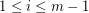 . A digraph is universal if for every pair of edges
. A digraph is universal if for every pair of edges 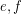 , there is an alternating walk containing both
, there is an alternating walk containing both  and
and 
Keywords: arc transitive; digraph
Woodall's Conjecture ★★★
Author(s): Woodall
 is a directed graph with smallest directed cut of size
is a directed graph with smallest directed cut of size  , then
, then  has
has  disjoint dijoins.
disjoint dijoins. The Two Color Conjecture ★★
Author(s): Neumann-Lara
 is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 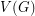 into
into 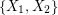 so that the graph induced by
so that the graph induced by 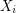 is acyclic for
is acyclic for 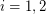 .
. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University