 login/create account
login/create account
Seymour, Paul D.
Fractional Hadwiger ★★
Author(s): Harvey; Reed; Seymour; Wood
 ,
,(a)
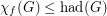
(b)
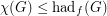
(c)
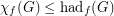 .
. Keywords: fractional coloring, minors
Seymour's r-graph conjecture ★★★
Author(s): Seymour
An  -graph is an
-graph is an  -regular graph
-regular graph  with the property that
with the property that 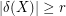 for every
for every 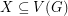 with odd size.
with odd size.
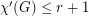 for every
for every  -graph
-graph  .
. Keywords: edge-coloring; r-graph
Non-edges vs. feedback edge sets in digraphs ★★★
Author(s): Chudnovsky; Seymour; Sullivan
For any simple digraph  , we let
, we let 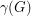 be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and
be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and 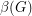 be the size of the smallest feedback edge set.
be the size of the smallest feedback edge set.
 is a simple digraph without directed cycles of length
is a simple digraph without directed cycles of length 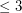 , then
, then 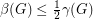 .
. Keywords: acyclic; digraph; feedback edge set; triangle free
Seagull problem ★★★
Author(s): Seymour
 vertex graph with no independent set of size
vertex graph with no independent set of size  has a complete graph on
has a complete graph on 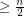 vertices as a minor.
vertices as a minor. Keywords: coloring; complete graph; minor
Seymour's Second Neighbourhood Conjecture ★★★
Author(s): Seymour
Keywords: Caccetta-Häggkvist; neighbourhood; second; Seymour
Bases of many weights ★★★
Let  be an (additive) abelian group, and for every
be an (additive) abelian group, and for every 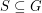 let
let 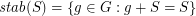 .
.
 be a matroid on
be a matroid on  , let
, let 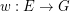 be a map, put
be a map, put 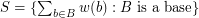 and
and 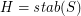 . Then
. Then 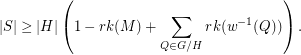
Alon-Saks-Seymour Conjecture ★★★
Author(s): Alon; Saks; Seymour
 is a simple graph which can be written as an union of
is a simple graph which can be written as an union of  edge-disjoint complete bipartite graphs, then
edge-disjoint complete bipartite graphs, then 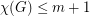 .
. Keywords: coloring; complete bipartite graph; eigenvalues; interlacing
Seymour's self-minor conjecture ★★★
Author(s): Seymour
Keywords: infinite graph; minor
Faithful cycle covers ★★★
Author(s): Seymour
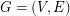 is a graph,
is a graph, 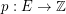 is admissable, and
is admissable, and 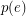 is even for every
is even for every 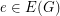 , then
, then 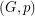 has a faithful cover.
has a faithful cover. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University