 login/create account
login/create account
zero sum
Pebbling a cartesian product ★★★
Author(s): Graham
We let 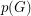 denote the pebbling number of a graph
denote the pebbling number of a graph  .
.
Conjecture 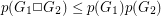 .
.
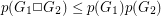 .
. Davenport's constant ★★★
Author(s):
For a finite (additive) abelian group  , the Davenport constant of
, the Davenport constant of  , denoted
, denoted 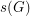 , is the smallest integer
, is the smallest integer  so that every sequence of elements of
so that every sequence of elements of  with length
with length 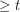 has a nontrivial subsequence which sums to zero.
has a nontrivial subsequence which sums to zero.
Conjecture 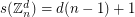
Keywords: Davenport constant; subsequence sum; zero sum
Bases of many weights ★★★
Let  be an (additive) abelian group, and for every
be an (additive) abelian group, and for every 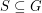 let
let 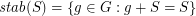 .
.
Conjecture Let  be a matroid on
be a matroid on  , let
, let 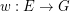 be a map, put
be a map, put 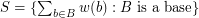 and
and 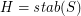 . Then
. Then 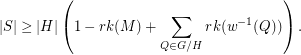
 be a matroid on
be a matroid on  , let
, let 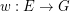 be a map, put
be a map, put 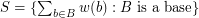 and
and 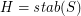 . Then
. Then 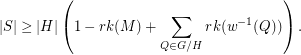
Gao's theorem for nonabelian groups ★★
Author(s): DeVos
For every finite multiplicative group  , let
, let 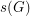 (
(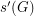 ) denote the smallest integer
) denote the smallest integer  so that every sequence of
so that every sequence of  elements of
elements of  has a subsequence of length
has a subsequence of length 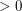 (length
(length 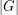 ) which has product equal to 1 in some order.
) which has product equal to 1 in some order.
Conjecture 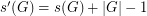 for every finite group
for every finite group  .
.
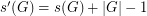 for every finite group
for every finite group  .
. Keywords: subsequence sum; zero sum
Few subsequence sums in Z_n x Z_n ★★
Conjecture For every 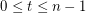 , the sequence in
, the sequence in 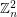 consisting of
consisting of 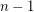 copes of
copes of 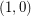 and
and  copies of
copies of 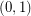 has the fewest number of distinct subsequence sums over all zero-free sequences from
has the fewest number of distinct subsequence sums over all zero-free sequences from 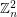 of length
of length 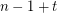 .
.
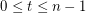 , the sequence in
, the sequence in 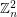 consisting of
consisting of 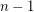 copes of
copes of 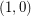 and
and  copies of
copies of 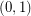 has the fewest number of distinct subsequence sums over all zero-free sequences from
has the fewest number of distinct subsequence sums over all zero-free sequences from 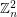 of length
of length 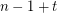 .
. Keywords: subsequence sum; zero sum
Olson's Conjecture ★★
Author(s): Olson
Conjecture If 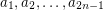 is a sequence of elements from a multiplicative group of order
is a sequence of elements from a multiplicative group of order  , then there exist
, then there exist 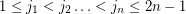 so that
so that 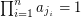 .
.
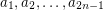 is a sequence of elements from a multiplicative group of order
is a sequence of elements from a multiplicative group of order  , then there exist
, then there exist 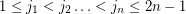 so that
so that 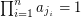 .
. Keywords: zero sum

 Drupal
Drupal CSI of Charles University
CSI of Charles University