 login/create account
login/create account
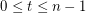 , the sequence in
, the sequence in 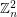 consisting of
consisting of 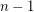 copes of
copes of 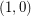 and
and  copies of
copies of 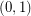 has the fewest number of distinct subsequence sums over all zero-free sequences from
has the fewest number of distinct subsequence sums over all zero-free sequences from 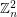 of length
of length 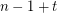 .
. Definition: Given a sequence  of elements from an additive abelian group, we call a subsequence sum any group element expressable as a sum of some nontrivial subsequence of
of elements from an additive abelian group, we call a subsequence sum any group element expressable as a sum of some nontrivial subsequence of  . We say that
. We say that  is zero-free if
is zero-free if  is not a subsequence sum.
is not a subsequence sum.
It is easy to see that every sequence 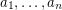 of elements from
of elements from 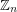 has a nontrivial subsequence which sums to zero (actually this holds for every group of order
has a nontrivial subsequence which sums to zero (actually this holds for every group of order  ). Just consider the elements
). Just consider the elements 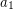 ,
,  ,
,  ,
, 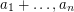 . If these elements are distinct, we have a zero sum. Otherwise, we have
. If these elements are distinct, we have a zero sum. Otherwise, we have 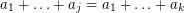 for some
for some 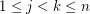 , but then
, but then 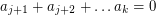 . The same argument shows that whenever
. The same argument shows that whenever 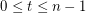 , every zero-free sequence of
, every zero-free sequence of  elements of
elements of 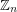 must have at least
must have at least  distinct subsequence sums. In other words, the sequence consisting of
distinct subsequence sums. In other words, the sequence consisting of  copies of
copies of 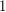 has the fewest number of distinct subsequence sums over all zero-free sequences in
has the fewest number of distinct subsequence sums over all zero-free sequences in 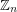 of length
of length  .
.
In the group 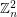 , a theorem of Olsen shows that every sequence of length
, a theorem of Olsen shows that every sequence of length 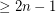 has a nontrivial subsequence which sums to zero. However, we do not know what the minimum number of distinct subsequence sums is for a zero-free sequence of a given length. The above conjecture would appear to be the natural optimum.
has a nontrivial subsequence which sums to zero. However, we do not know what the minimum number of distinct subsequence sums is for a zero-free sequence of a given length. The above conjecture would appear to be the natural optimum.

 Drupal
Drupal CSI of Charles University
CSI of Charles University