 login/create account
login/create account
We let 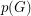 denote the pebbling number of a graph
denote the pebbling number of a graph  .
.
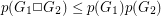 .
. The pebbling number of a graph  , denoted
, denoted 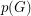 , is the smallest integer
, is the smallest integer  so that however
so that however  pebbles are distributed onto the vertices of
pebbles are distributed onto the vertices of  , it is possible to move a pebble to any vertex by a sequence of steps, where in each step we remove two pebbles from one vertex, and then place one on an adjacent vertex. The cartesian product of two graphs
, it is possible to move a pebble to any vertex by a sequence of steps, where in each step we remove two pebbles from one vertex, and then place one on an adjacent vertex. The cartesian product of two graphs  and
and  , denoted
, denoted 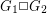 , is the graph with vertex set
, is the graph with vertex set 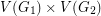 and an edge from
and an edge from 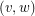 to
to 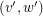 if either
if either 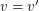 and
and 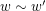 (in
(in  ) or
) or 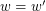 and
and 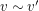 (in
(in  ).
).
Graph Pebbling arose out of the study of zero-sum subsequences in groups, but has proved to be a rich and interesting topic in graph theory. See Glenn Hurlbert's wonderful graph pebbling page for much more on this topic (and this problem in particular). Graham's conjecture was stated in one of the first papers on this subject by Fan Chung [C], and has since generated considerable interest.
There are a number of partial results toward this conjecture. Chung [C] proved that 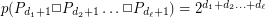 , thus settling the conjecture for products of paths (here
, thus settling the conjecture for products of paths (here 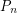 denotes a path with
denotes a path with  vertices). It is also known when
vertices). It is also known when 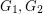 are both trees, both cycles, and for graphs with high minimum degree. Again, we encourage the interested reader to see the graph pebbling page for more details.
are both trees, both cycles, and for graphs with high minimum degree. Again, we encourage the interested reader to see the graph pebbling page for more details.
Bibliography
*[C] F. Chung, Pebbling in hypercubes SIAM J. Disc. Math. 2 (1989), 467--472.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University