 login/create account
login/create account
matroid
Aharoni-Berger conjecture ★★★
Conjecture If 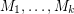 are matroids on
are matroids on  and
and 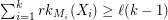 for every partition
for every partition  of
of  , then there exists
, then there exists 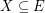 with
with 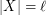 which is independent in every
which is independent in every 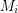 .
.
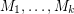 are matroids on
are matroids on  and
and 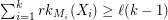 for every partition
for every partition  of
of  , then there exists
, then there exists 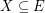 with
with 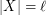 which is independent in every
which is independent in every 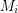 .
. Keywords: independent set; matroid; partition
Bases of many weights ★★★
Let  be an (additive) abelian group, and for every
be an (additive) abelian group, and for every 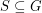 let
let 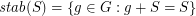 .
.
Conjecture Let  be a matroid on
be a matroid on  , let
, let 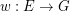 be a map, put
be a map, put 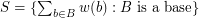 and
and 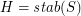 . Then
. Then 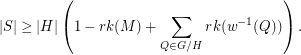
 be a matroid on
be a matroid on  , let
, let 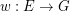 be a map, put
be a map, put 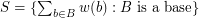 and
and 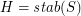 . Then
. Then 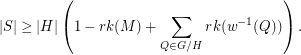
Rota's unimodal conjecture ★★★
Author(s): Rota
Let  be a matroid of rank
be a matroid of rank  , and for
, and for 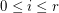 let
let 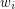 be the number of closed sets of rank
be the number of closed sets of rank 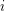 .
.
Conjecture 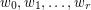 is unimodal.
is unimodal.
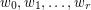 is unimodal.
is unimodal. Conjecture 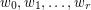 is log-concave.
is log-concave.
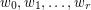 is log-concave.
is log-concave. Keywords: flat; log-concave; matroid

 Drupal
Drupal CSI of Charles University
CSI of Charles University