Home » Subject » Number Theory » Combinatorial N.T.
Importance: Medium ✭✭
Author(s): Olson, John E.
Subject: Number Theory
» Combinatorial Number Theory
Keywords: zero sum
Recomm. for undergrads: no
Prize: none
Posted by: mdevos
on: March 10th, 2007
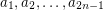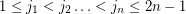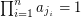Conjecture   If $ a_1,a_2,\ldots,a_{2n-1} $ is a sequence of elements from a multiplicative group of order $ n $, then there exist $ 1 \le j_1 < j_2 \ldots < j_n \le 2n-1 $ so that $ \prod_{i=1}^n a_{j_i} = 1 $.

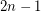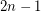A famous theorem of Erdos, Ginzburg, and Ziv asserts that every sequence of $ 2n-1 $ elements from an additive abelian group has a subsequence of length $ n $ which sums to $ 0 $. This pretty result has lead to numerous generalizations. 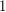In particular, Olsen generalized this result by showing that every sequence of $ 2n-1 $ elements from an arbitrary multiplicative group of order $ n $ has a subsequence of length $ n $ which has product equal to $ 1 $ in some order. The above conjecture asserts that this reordering is not needed. Apart from Olson's result, there appears to be very little known about this problem. Next we highlight an obvious question which appears untouched.

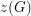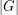For every finite multiplicative group $ G $, let $ z(G) $ denote the smallest integer $ m $ so that every sequence of $ m $ elements of $ G $ has a subsequence of length $ |G| $ with product equal to 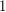$ 1 $ in the given order (so Olsen's conjecture is equivalent to 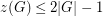$ z(G) \le 2|G|-1 $). It is clear that 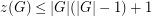$ z(G) \le |G|(|G|-1) + 1 $, since any sequence of length 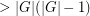$ > |G|(|G|-1) $ must contain at least 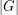$ |G| $ copies of the same element, and the product of these will be 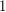$ 1 $. However, I (M. DeVos) don't know how to improve significantly on this upper bound, and it would appear to me that any significant progress in this direction would require a little something new.

add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options