 login/create account
login/create account
Faithful cycle covers
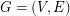 is a graph,
is a graph, 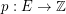 is admissable, and
is admissable, and 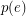 is even for every
is even for every 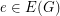 , then
, then 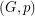 has a faithful cover.
has a faithful cover. Definition: Let 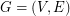 be a graph and let
be a graph and let 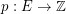 . A list
. A list 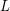 of cycles of
of cycles of  is a faithful (cycle) cover of
is a faithful (cycle) cover of 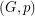 if every edge
if every edge  of
of  occurs in exactly
occurs in exactly 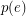 cycles of
cycles of 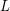 . Thus, the cycle double cover conjecture is equivalent to the statement that
. Thus, the cycle double cover conjecture is equivalent to the statement that 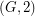 has a faithful cover for every graph
has a faithful cover for every graph  with no bridge. We define the map
with no bridge. We define the map  to be admissable if
to be admissable if 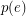 satisfies the following properties:
satisfies the following properties:
i  is nonnegative.
is nonnegative.
ii 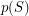 is even for every edge-cut
is even for every edge-cut  .
.
iii 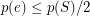 for every edge-cut
for every edge-cut  and edge
and edge 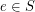 .
.
It is easy to see that  has a faithful cover only if
has a faithful cover only if  is admissable. However, the converse is false. A counterexample is obtained by taking the Petersen graph, putting weight
is admissable. However, the converse is false. A counterexample is obtained by taking the Petersen graph, putting weight  on the edges of a perfect matching, and
on the edges of a perfect matching, and 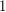 elsewhere.
elsewhere.
More generally, for a graph G=(V,E), one may consider the vector space of real numbers indexed by E. We associate every circuit C with its incidence vector. Most of the basic questions about this space are solved. Seymour [S] has shown that a vector p can be written as a nonnegative rational combination of cycles if and only if it satisfies conditions (i) and (iii) in the definition of admissable. It is an easy exercise to show that for a 3-edge-connected graph G, a vector p can be written as an integer combination of cycles if and only if p satisfies (ii) in the definition of admissable. Seymour's conjecture is equivalent to the statement that every admissable map may be realized as a half-integer combination of circuits. Note the similarity of this to The Berge-Fulkerson conjecture.
The most interesting result about faithful covers is a theorem of Alspach, Goddyn, and Zhang which resolved a conjecture of Seymour. They prove that whenever  has no minor isomorphic to Petersen, every admissable map has a corresponding faithful cover. For a general graph
has no minor isomorphic to Petersen, every admissable map has a corresponding faithful cover. For a general graph  with no bridge, Bermond, Jackson, and Jaeger [BJJ] proved that
with no bridge, Bermond, Jackson, and Jaeger [BJJ] proved that 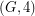 has a faithful cover and Fan [F] proveed that
has a faithful cover and Fan [F] proveed that 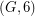 has a faithful cover. DeVos, Johnson, and Seymour [DJS] proved that
has a faithful cover. DeVos, Johnson, and Seymour [DJS] proved that 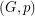 has a faithful cover whenever
has a faithful cover whenever  is admissable and there is a nonnegative integer
is admissable and there is a nonnegative integer  such that
such that 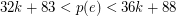 holds for every edge
holds for every edge  . However, little else seems to be known. In particular, it does not appear to be known if there exist integers
. However, little else seems to be known. In particular, it does not appear to be known if there exist integers 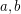 with
with 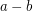 arbitrarily large so that
arbitrarily large so that 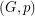 has a faithful cover whenever
has a faithful cover whenever  is an admissable function taking on only the values
is an admissable function taking on only the values 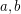 . Such a result would appear to require an idea not contained in any of the aforementioned papers.
. Such a result would appear to require an idea not contained in any of the aforementioned papers.
The analogous problem for oriented circuit covers does not appear to be very promising. It is easy to see that for an orientation of a series parallel graph G and a map 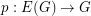 which satisfies the obvious conditions, that
which satisfies the obvious conditions, that 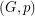 will have a circuit cover using every edge in its given direction. However, even with a
will have a circuit cover using every edge in its given direction. However, even with a 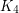 minor, there is a great deal of forcing, and nothing much looks like it would be true.
minor, there is a great deal of forcing, and nothing much looks like it would be true.
Bibliography
\[AGZ] B. Alspach, L. Goddyn, and C-Q Zhang, Graphs with the circuit cover property, Trans. Amer. Math. Soc., 344 (1994), 131-154. MathSciNet
[BJJ] J.C. Bermond, B. Jackson, and F. Jaeger, Shortest covering of graphs with cycles, J. Combinatorial Theory Ser. B 35 (1983), 297-308. MathSciNet
[DJS] M. DeVos, T. Johnson, P.D. Seymour, Cut-coloring and circuit covering
[F] G. Fan, Integer flows and cycle covers, J. Combinatorial Theory Ser. B 54 (1992), 113-122. MathSciNet
[S] P.D. Seymour, Sums of circuits in Graph Theory and Related Topics edited by J.A. Bondy and U.S.R. Murty, Academic Press, New York/Berlin (1979), 341-355. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University