Home » Author index

Alon, Noga


Graph Theory » Directed Graphs

Arc-disjoint directed cycles in regular directed graphs ★★

Author(s): Alon; McDiarmid; Molloy

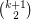Conjecture   If $ G $ is a $ k $-regular directed graph with no parallel arcs, then $ G $ contains a collection of $ {k+1 \choose 2} $ arc-disjoint directed cycles.

Keywords:

Posted by fhavet
updated May 17th, 2013
add new comment
Graph Theory » Graph Algorithms

PTAS for feedback arc set in tournaments ★★

Author(s): Ailon; Alon

Question   Is there a polynomial time approximation scheme for the feedback arc set problem for the class of tournaments?

Keywords: feedback arc set; PTAS; tournament

Posted by fhavet
updated March 15th, 2013
add new comment
Graph Theory » Coloring » Vertex coloring

List chromatic number and maximum degree of bipartite graphs ★★

Author(s): Alon

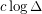Conjecture   There is a constant $ c $ such that the list chromatic number of any bipartite graph $ G $ of maximum degree $ \Delta $ is at most $ c \log \Delta $.

Keywords:

Posted by fhavet
updated March 12th, 2013
add new comment
Graph Theory » Directed Graphs

Splitting a digraph with minimum outdegree constraints ★★★

Author(s): Alon

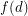Problem   Is there a minimum integer $ f(d) $ such that the vertices of any digraph with minimum outdegree $ d $ can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least $ d $?

Keywords:

Posted by fhavet
updated March 1st, 2013
add new comment
Graph Theory » Basic G.T.

Nearly spanning regular subgraphs ★★★

Author(s): Alon; Mubayi

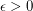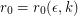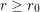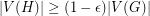Conjecture   For every $ \epsilon > 0 $ and every positive integer $ k $, there exists $ r_0 = r_0(\epsilon,k) $ so that every simple $ r $-regular graph $ G $ with $ r \ge r_0 $ has a $ k $-regular subgraph $ H $ with $ |V(H)| \ge (1- \epsilon) |V(G)| $.

Keywords: regular; subgraph

Posted by mdevos
updated May 22nd, 2008
add new comment
Combinatorics

Even vs. odd latin squares ★★★

Author(s): Alon; Tarsi

A latin square is even if the product of the signs of all of the row and column permutations is 1 and is odd otherwise.

Conjecture   For every positive even integer $ n $, the number of even latin squares of order $ n $ and the number of odd latin squares of order $ n $ are different.

Keywords: latin square

Posted by mdevos
updated October 7th, 2007
add new comment
Graph Theory » Algebraic G.T.

Ramsey properties of Cayley graphs ★★★

Author(s): Alon

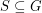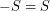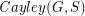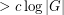Conjecture   There exists a fixed constant $ c $ so that every abelian group $ G $ has a subset $ S \subseteq G $ with $ -S = S $ so that the Cayley graph $ {\mathit Cayley}(G,S) $ has no clique or independent set of size $ > c \log |G| $.

Keywords: Cayley graph; Ramsey number

Posted by mdevos
updated June 10th, 2007
add new comment
Graph Theory » Coloring » Vertex coloring

Alon-Saks-Seymour Conjecture ★★★

Author(s): Alon; Saks; Seymour

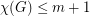Conjecture   If $ G $ is a simple graph which can be written as an union of $ m $ edge-disjoint complete bipartite graphs, then $ \chi(G) \le m+1 $.

Keywords: coloring; complete bipartite graph; eigenvalues; interlacing

Posted by mdevos
updated February 26th, 2010
1 comment
Graph Theory » Topological G.T. » Coloring

Bounded colorings for planar graphs ★★

Author(s): Alon; Ding; Oporowski; Vertigan

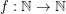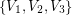Question   Does there exists a fixed function $ f : {\mathbb N} \rightarrow {\mathbb N} $ so that every planar graph of maximum degree $ d $ has a partition of its vertex set into at most three sets $ \{V_1,V_2,V_3\} $ so that for 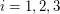$ i=1,2,3 $, every component of the graph induced by 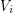$ V_i $ has size at most $ f(d) $?

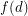Keywords: coloring; partition; planar graph

Posted by mdevos
updated May 23rd, 2007
add new comment
Graph Theory » Coloring » Vertex coloring

Strong colorability ★★★

Author(s): Aharoni; Alon; Haxell

Let $ r $ be a positive integer. We say that a graph $ G $ is strongly $ r $-colorable if for every partition of the vertices to sets of size at most $ r $ there is a proper $ r $-coloring of $ G $ in which the vertices in each set of the partition have distinct colors.

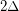Conjecture   If $ \Delta $ is the maximal degree of a graph $ G $, then $ G $ is strongly $ 2 \Delta $-colorable.

Keywords: strong coloring

Posted by berger
updated November 19th, 2009
5 comments
Syndicate content