 login/create account
login/create account
Vertigan, Dirk
Bounded colorings for planar graphs ★★
Author(s): Alon; Ding; Oporowski; Vertigan
Question Does there exists a fixed function 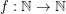 so that every planar graph of maximum degree
so that every planar graph of maximum degree  has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets 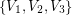 so that for
so that for 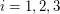 , every component of the graph induced by
, every component of the graph induced by 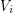 has size at most
has size at most 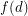 ?
?
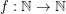 so that every planar graph of maximum degree
so that every planar graph of maximum degree  has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets 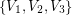 so that for
so that for 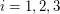 , every component of the graph induced by
, every component of the graph induced by 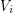 has size at most
has size at most 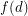 ?
? Keywords: coloring; partition; planar graph

 Drupal
Drupal CSI of Charles University
CSI of Charles University