 login/create account
login/create account
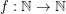 so that every planar graph of maximum degree
so that every planar graph of maximum degree  has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets 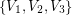 so that for
so that for 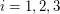 , every component of the graph induced by
, every component of the graph induced by 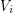 has size at most
has size at most 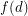 ?
? An ordinary  -coloring of a graph, is a partition the vertex set into at most
-coloring of a graph, is a partition the vertex set into at most  sets
sets 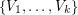 so that each
so that each 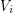 induces a subgraph where every component is an isolated vertex. Here we are considering a relaxation of this where we insist only that each
induces a subgraph where every component is an isolated vertex. Here we are considering a relaxation of this where we insist only that each 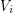 induces a subgraph where every component has bounded size. This type of coloring was first suggested by Ding, Oporowski, and Vertigan and has already lead to some interesting results see [ADOV] and [HSzT].
induces a subgraph where every component has bounded size. This type of coloring was first suggested by Ding, Oporowski, and Vertigan and has already lead to some interesting results see [ADOV] and [HSzT].
It follows from the four color theorem that every planar graph has a vertex partition into four sets  so that every component of a subgraph induced by some
so that every component of a subgraph induced by some 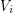 has size at most 1. On the other hand, Alon, Ding, Oporowski, and Vertigan construct for every integer
has size at most 1. On the other hand, Alon, Ding, Oporowski, and Vertigan construct for every integer  a planar graph
a planar graph 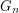 with the property that for every partition of
with the property that for every partition of 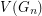 into
into 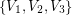 , some component of a subgraph induced by some
, some component of a subgraph induced by some 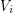 will have size
will have size 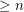 . The construction is easy to give: Let
. The construction is easy to give: Let  be the graph obtained from a path
be the graph obtained from a path  of length
of length 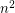 by adding a new vertex
by adding a new vertex  adjacent to every vertex of this path. Now, form the graph
adjacent to every vertex of this path. Now, form the graph 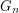 from
from  disjoint copies of
disjoint copies of  by adding a new vertex
by adding a new vertex  joined to every old vertex. Note that
joined to every old vertex. Note that 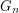 is planar as required. Let us assume (for a contradiction) that
is planar as required. Let us assume (for a contradiction) that 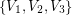 is a partition of
is a partition of 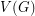 with the property that every component of a subgraph induced by
with the property that every component of a subgraph induced by 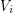 has size
has size 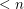 . We may assume without loss that
. We may assume without loss that 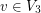 , but then there are at most
, but then there are at most 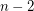 other vertices in
other vertices in 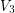 , so there is a copy of
, so there is a copy of  which contains no vertices in
which contains no vertices in 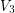 . We may assume that the vertex
. We may assume that the vertex  in this copy is in the set
in this copy is in the set 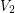 , but then at most
, but then at most 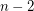 other vertices in the corresponding copy of
other vertices in the corresponding copy of  are in
are in 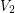 . It now follows that there is a subpath of this copy of
. It now follows that there is a subpath of this copy of  of length
of length 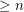 in which all vertices are in
in which all vertices are in 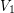 . This completes the proof. The above question asks if such a family can still be constructed with the additional constraint that all vertices have bounded degree.
. This completes the proof. The above question asks if such a family can still be constructed with the additional constraint that all vertices have bounded degree.
In 2013, this question was answered in the affirmative by Louis Esperet and Gwenaël Joret [EJ].
Bibliography
*[ADOV] Alon, Noga; Ding, Guoli; Oporowski, Bogdan; Vertigan, Dirk, Partitioning into graphs with only small components, J. Combin. Theory Ser. B 87 (2003), no. 2, 231--243. MathSciNet
[HSzT] Haxell, Penny; Szabó, Tibor; Tardos, Gábor, Bounded size components - partitions and transversals. J. Combin. Theory Ser. B 88 (2003), no. 2, 281--297. MathSciNet
[EJ] Louis Esperet, Gwenaël Joret. Coloring planar graphs with three colors and no large monochromatic components, arXiv:1303.2487, 2013.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University