 login/create account
login/create account
planar graph
Obstacle number of planar graphs ★
Author(s): Alpert; Koch; Laison
Does there exist a planar graph with obstacle number greater than 1? Is there some  such that every planar graph has obstacle number at most
such that every planar graph has obstacle number at most  ?
?
Keywords: graph drawing; obstacle number; planar graph; visibility graph
Finding k-edge-outerplanar graph embeddings ★★
Author(s): Bentz
 -outerplanar embedding for which
-outerplanar embedding for which  is minimal can be found in polynomial time. Does a similar result hold for
is minimal can be found in polynomial time. Does a similar result hold for  -edge-outerplanar graphs?
-edge-outerplanar graphs? Keywords: planar graph; polynomial algorithm
Approximation ratio for k-outerplanar graphs ★★
Author(s): Bentz
 -outerplanar graphs or tree-width graphs?
-outerplanar graphs or tree-width graphs? Keywords: approximation algorithms; planar graph; polynomial algorithm
Approximation Ratio for Maximum Edge Disjoint Paths problem ★★
Author(s): Bentz
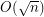 be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than
be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than 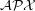 -hardness?
-hardness? Keywords: approximation algorithms; Disjoint paths; planar graph; polynomial algorithm
Domination in plane triangulations ★★
 has a dominating set of size
has a dominating set of size 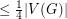 .
. Keywords: coloring; domination; multigrid; planar graph; triangulation
5-coloring graphs with small crossing & clique numbers ★★
For a graph  , we let
, we let 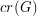 denote the crossing number of
denote the crossing number of  , and we let
, and we let 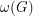 denote the size of the largest complete subgraph of
denote the size of the largest complete subgraph of  .
.
 with
with 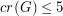 and
and 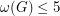 have a 5-coloring?
have a 5-coloring? Keywords: coloring; crossing number; planar graph
Jones' conjecture ★★
For a graph  , let
, let 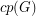 denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let
denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let 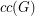 denote the cardinality of a minimum feedback vertex set (set of vertices
denote the cardinality of a minimum feedback vertex set (set of vertices 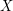 so that
so that 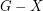 is acyclic).
is acyclic).
 ,
, 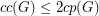 .
. Keywords: cycle packing; feedback vertex set; planar graph
Oriented chromatic number of planar graphs ★★
Author(s):
An oriented colouring of an oriented graph is assignment  of colours to the vertices such that no two arcs receive ordered pairs of colours
of colours to the vertices such that no two arcs receive ordered pairs of colours 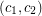 and
and 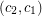 . It is equivalent to a homomorphism of the digraph onto some tournament of order
. It is equivalent to a homomorphism of the digraph onto some tournament of order  .
.
Keywords: oriented coloring; oriented graph; planar graph
Mapping planar graphs to odd cycles ★★★
Author(s): Jaeger
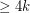 has a homomorphism to
has a homomorphism to 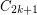 .
. Keywords: girth; homomorphism; planar graph
Circular coloring triangle-free subcubic planar graphs ★★
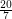 ?
? Keywords: circular coloring; planar graph; triangle free

 Drupal
Drupal CSI of Charles University
CSI of Charles University