 login/create account
login/create account
latin square
Hall-Paige conjecture ★★★
A complete map for a (multiplicative) group  is a bijection
is a bijection 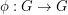 so that the map
so that the map 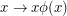 is also a bijection.
is also a bijection.
Conjecture If  is a finite group and the Sylow 2-subgroups of
is a finite group and the Sylow 2-subgroups of  are either trivial or non-cyclic, then
are either trivial or non-cyclic, then  has a complete map.
has a complete map.
 is a finite group and the Sylow 2-subgroups of
is a finite group and the Sylow 2-subgroups of  are either trivial or non-cyclic, then
are either trivial or non-cyclic, then  has a complete map.
has a complete map. Keywords: complete map; finite group; latin square
Snevily's conjecture ★★★
Author(s): Snevily
Conjecture Let  be an abelian group of odd order and let
be an abelian group of odd order and let 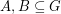 satisfy
satisfy 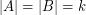 . Then the elements of
. Then the elements of  and
and 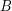 may be ordered
may be ordered 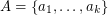 and
and 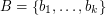 so that the sums
so that the sums 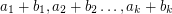 are pairwise distinct.
are pairwise distinct.
 be an abelian group of odd order and let
be an abelian group of odd order and let 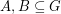 satisfy
satisfy 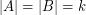 . Then the elements of
. Then the elements of  and
and 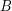 may be ordered
may be ordered 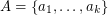 and
and 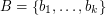 so that the sums
so that the sums 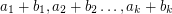 are pairwise distinct.
are pairwise distinct. Keywords: addition table; latin square; transversal
Even vs. odd latin squares ★★★
A latin square is even if the product of the signs of all of the row and column permutations is 1 and is odd otherwise.
Conjecture For every positive even integer  , the number of even latin squares of order
, the number of even latin squares of order  and the number of odd latin squares of order
and the number of odd latin squares of order  are different.
are different.
 , the number of even latin squares of order
, the number of even latin squares of order  and the number of odd latin squares of order
and the number of odd latin squares of order  are different.
are different. Keywords: latin square

 Drupal
Drupal CSI of Charles University
CSI of Charles University