 login/create account
login/create account
Snevily, Hunter S.
Roller Coaster permutations ★★★
Let 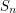 denote the set of all permutations of
denote the set of all permutations of ![$ [n]=\set{1,2,\ldots,n} $](/files/tex/470bd09059264370b76b4da90b77dc370c7e0e7c.png) . Let
. Let 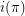 and
and 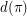 denote respectively the number of increasing and the number of decreasing sequences of contiguous numbers in
denote respectively the number of increasing and the number of decreasing sequences of contiguous numbers in  . Let
. Let 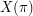 denote the set of subsequences of
denote the set of subsequences of  with length at least three. Let
with length at least three. Let 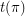 denote
denote 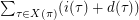 .
.
A permutation 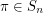 is called a Roller Coaster permutation if
is called a Roller Coaster permutation if 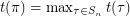 . Let
. Let 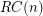 be the set of all Roller Coaster permutations in
be the set of all Roller Coaster permutations in 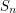 .
.
Conjecture For 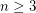 ,
,
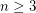 ,
,- \item If
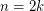 , then
, then 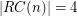 . \item If
. \item If 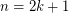 , then
, then 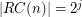 with
with 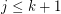 .
. Conjecture (Odd Sum conjecture) Given 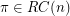 ,
,
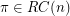 ,
,- \item If
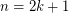 , then
, then 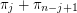 is odd for
is odd for 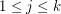 . \item If
. \item If 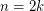 , then
, then 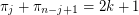 for all
for all 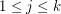 .
. Keywords:
Snevily's conjecture ★★★
Author(s): Snevily
Conjecture Let  be an abelian group of odd order and let
be an abelian group of odd order and let 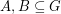 satisfy
satisfy 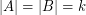 . Then the elements of
. Then the elements of  and
and 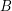 may be ordered
may be ordered 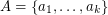 and
and 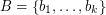 so that the sums
so that the sums 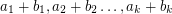 are pairwise distinct.
are pairwise distinct.
 be an abelian group of odd order and let
be an abelian group of odd order and let 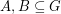 satisfy
satisfy 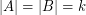 . Then the elements of
. Then the elements of  and
and 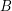 may be ordered
may be ordered 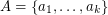 and
and 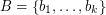 so that the sums
so that the sums 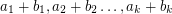 are pairwise distinct.
are pairwise distinct. Keywords: addition table; latin square; transversal

 Drupal
Drupal CSI of Charles University
CSI of Charles University