 login/create account
login/create account
A complete map for a (multiplicative) group  is a bijection
is a bijection 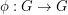 so that the map
so that the map 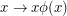 is also a bijection.
is also a bijection.
 is a finite group and the Sylow 2-subgroups of
is a finite group and the Sylow 2-subgroups of  are either trivial or non-cyclic, then
are either trivial or non-cyclic, then  has a complete map.
has a complete map. The motivation for this problem comes from the study of Latin Squares. Call a collection of  cells from a
cells from a 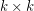 matrix a transversal if there is exactly one cell from each row and one from each column, and say that a transversal is latin if no two of its cells contain the same element. The multiplication table of every (finite multiplicative) group
matrix a transversal if there is exactly one cell from each row and one from each column, and say that a transversal is latin if no two of its cells contain the same element. The multiplication table of every (finite multiplicative) group  is a latin square, and we see that
is a latin square, and we see that  has a latin transversal if and only if it has a complete map (the cells indexed by
has a latin transversal if and only if it has a complete map (the cells indexed by 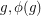 form the transversal). If we do have such a latin transversal, then for every
form the transversal). If we do have such a latin transversal, then for every 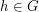 , the map
, the map 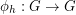 given by
given by 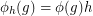 is also a latin transversal, and the collection
is also a latin transversal, and the collection 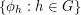 gives us
gives us 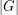 pairwise disjoint latin transversals in the multiplication table of
pairwise disjoint latin transversals in the multiplication table of  . This is precisely equivalent to the existence of a latin square orthogonal to this multiplication table. Thus, the above conjecture may be restated as follows.
. This is precisely equivalent to the existence of a latin square orthogonal to this multiplication table. Thus, the above conjecture may be restated as follows.
 is a finite group and the Sylow 2-subgroups of
is a finite group and the Sylow 2-subgroups of  are either trivial or non-cyclic, then there is a latin square orthogonal to the multiplication table of
are either trivial or non-cyclic, then there is a latin square orthogonal to the multiplication table of  .
. Next, let us show that the assumption in the conjecture on Sylow 2-subgroups is necessary, so let  be a group with nontrivial cyclic 2-Sylow subgroup
be a group with nontrivial cyclic 2-Sylow subgroup  . Under these assumptions, it follows from a theorem of Burnside that there exists a normal subgroup
. Under these assumptions, it follows from a theorem of Burnside that there exists a normal subgroup 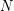 (of odd order) so that
(of odd order) so that 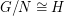 . Let
. Let 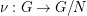 be the canonical homomorphism and let
be the canonical homomorphism and let  be the unique element in
be the unique element in 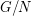 of order 2. Now, suppose (for a contradiction) that
of order 2. Now, suppose (for a contradiction) that  has a complete map
has a complete map 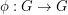 and consider the three families
and consider the three families 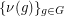 ,
, 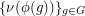 ,
, 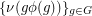 , and their products
, and their products 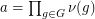 ,
, 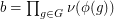 , and
, and 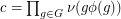 . For every
. For every 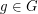 we have
we have 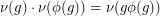 , so taking the product of all of these equations we get
, so taking the product of all of these equations we get 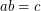 (since
(since 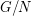 is abelian, the order doesn't matter here). However, every element in
is abelian, the order doesn't matter here). However, every element in 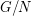 occurs exactly
occurs exactly 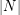 times in each of these families, and it follows from this that
times in each of these families, and it follows from this that 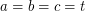 , giving us a contradiction.
, giving us a contradiction.
Hall and Paige proved their conjecture for solvable groups, and for the alternating and symmetric groups. More recently, a number of authors have studied this problem, establishing a number of partial results. Dalla Volta and Gavioli [DG3] have shown that a minimal counterexample to the conjecture is either almost simple, or it has a unique central involution and its derived subgroup is is a quasi-simple group of index 2. The following list contains a number groups for which the problem is solved.
- \item
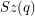 ,
, 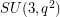 ,
, 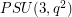 where
where 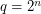 and
and 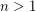 [D] \item
[D] \item 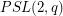 ,
, 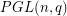 ,
, 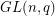 with
with 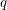 odd [DG1] [DG2] \item
odd [DG1] [DG2] \item 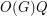 where
where 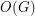 is the largest normal subgroup of odd order and
is the largest normal subgroup of odd order and 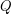 is a Frobenius complement [D] \item
is a Frobenius complement [D] \item 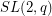 [E2] [E3] [S] \item
[E2] [E3] [S] \item 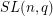 ,
, 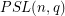 ,
, 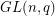 ,
, 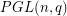 with
with 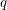 even and
even and 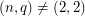 [DG1] \item Matthieu groups and their automorphism groups [DG1]
[DG1] \item Matthieu groups and their automorphism groups [DG1] The Hall-Paige conjecture is rather trivial for abelian groups, but Snevily has suggested an interesting conjecture concerning latin transversals in submatricies of the latin squares given by multiplication tables in abelian groups. There is a common generalization of these two conjectures highlighted below. I (M. DeVos) have no reason to suggest this conjecture other than its natural appearance, so it may well be false already for some small examples.
 be a group and let
be a group and let 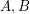 be subsets of
be subsets of  with
with 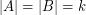 . Then there exists an ordering
. Then there exists an ordering 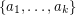 of
of  and
and 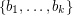 of
of 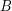 so that the products
so that the products 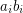 are distinct unless there is a subgroup
are distinct unless there is a subgroup 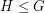 so that the Sylow 2-subgroups of
so that the Sylow 2-subgroups of  are nontrivial and cyclic, and there exist
are nontrivial and cyclic, and there exist 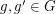 so that
so that 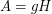 and
and 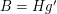 .
. Bibliography
[W] Wilcox, Stewart, Reduction of the Hall-Paige conjecture to sporadic simple groups, J. Algebra 321 (2009), no. 5, 1407--1428. MathSciNet
[DG1] F. Dalla Volta, N. Gavioli, Complete mappings in some linear and projective groups, Arch. Math. (Basel) 61 (1993) 111--118. MathSciNet.
[DG2] F. Dalla Volta, N. Gavioli, On the admissibility of some linear and projective groups in odd characteristic, Geom. Dedicata 66 (1997) 245--254. MathSciNet.
[DG3] F. Dalla Volta, N. Gavioli, N. Minimal counterexamples to a conjecture of Hall and Paige. Arch. Math. (Basel) 77 (2001), no. 3, 209--214. MathSciNet.
[D] O. M. Di Vincenzo, On the existence of complete mappings of finite groups. Rend. Mat. 9, 7, 189--198 (1989). MathSciNet.
[E1] A.B. Evans, The existence of complete mappings of finite groups, Congr. Numer. 90 (1992) 65--75. MathSciNet.
[E2] A.B. Evans, The existence of complete mappings of 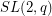 ,
, 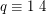 , Finite Fields Appl. 7 (2001) 373--381. MathSciNet.
, Finite Fields Appl. 7 (2001) 373--381. MathSciNet.
[E3] A. B. Evans, The existence of complete mappings of 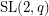 ,
, 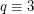 modulo 4. Finite Fields Appl. 11 (2005), no. 1, 151--155. MathSciNet.
modulo 4. Finite Fields Appl. 11 (2005), no. 1, 151--155. MathSciNet.
*[HP] M. Hall, L. J. Paige, Complete mappings of finite groups, Pacific J. Math. 5 (1955) 541--549. MathSciNet.
[S] D. Saeli, Saeli applicazioni complete e rapporto incrementale in doppi cappi. Riv. Mat. Univ. Parma 15, 4, 11--117 (1989). MathSciNet.
[WV] M. Vaughan-Lee, I. M. Wanless, Latin squares and the Hall-Paige conjecture. Bull. London Math. Soc. 35 (2003), no. 2, 191--195. MathSciNet.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University