Splitting a digraph with minimum outdegree constraints

Importance: High ✭✭✭

Author(s):

Subject:	Graph Theory
	» Directed Graphs

Keywords:

Recomm. for undergrads: no

Posted	by:	fhavet
	on:	March 1st, 2013

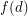Problem Is there a minimum integer $f(d)$ such that the vertices of any digraph with minimum outdegree $d$ can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least $d$ ?

Thomassen [T] proved the conjecture when 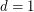$d=1$ and showed 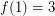$f(1)=3$ . In fact, this case is equivalent to the case 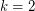$k=2$ of the Bermond-Thomassen Conjecture.

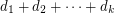The existence of the corresponding function $f$ for the undirected analogue is easy and has been observed by many authors. 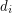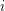Stiebitz [S] even proved the following tight result: if the minimum degree of an undirected graph $G$ is $d_1+d_2+ \cdots + d_k$ , where each $d_i$ is a non-negative integer, then the vertex set of $G$ can be partitioned into $k$ pairwise disjoint sets $V_1,\dots , V_k$ , so that for all $i$ , the induced subgraph on 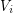$V_i$ has minimum degree at least 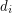$d_i$ . This is clearly tight, as shown by an appropriate complete graph.