 login/create account
login/create account
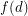 such that the vertices of any digraph with minimum outdegree
such that the vertices of any digraph with minimum outdegree  can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least
can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least  ?
? Thomassen [T] proved the conjecture when 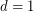 and showed
and showed 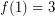 . In fact, this case is equivalent to the case
. In fact, this case is equivalent to the case 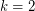 of the Bermond-Thomassen Conjecture.
of the Bermond-Thomassen Conjecture.
The existence of the corresponding function  for the undirected analogue is easy and has been observed by many authors. Stiebitz [S] even proved the following tight result: if the minimum degree of an undirected graph
for the undirected analogue is easy and has been observed by many authors. Stiebitz [S] even proved the following tight result: if the minimum degree of an undirected graph  is
is 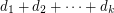 , where each
, where each 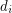 is a non-negative integer, then the vertex set of
is a non-negative integer, then the vertex set of  can be partitioned into
can be partitioned into  pairwise disjoint sets
pairwise disjoint sets  , so that for all
, so that for all 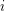 , the induced subgraph on
, the induced subgraph on 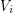 has minimum degree at least
has minimum degree at least 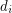 . This is clearly tight, as shown by an appropriate complete graph.
. This is clearly tight, as shown by an appropriate complete graph.
Bibliography
*[A] Noga Alon, Disjoint Directed Cycles, Journal of Combinatorial Theory, Series B, 68 (1996), no. 2, 167-178.
[S] M. Stiebitz, Decomposing graphs under degree constraints, J. Graph Theory 23 (1996), 31-324.
[T] C. Thomassen, Disjoint cycles in digraphs, Combinatorica 3 (1983), 393 - 396.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University