Home » Subject » Graph Theory » Coloring » Vertex coloring

List chromatic number and maximum degree of bipartite graphs

Importance: Medium ✭✭
Author(s): Alon, Noga
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 12th, 2013
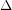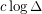Conjecture   There is a constant $ c $ such that the list chromatic number of any bipartite graph $ G $ of maximum degree $ \Delta $ is at most $ c \log \Delta $.

For definitions and an introduction to list colouring, see the related Wikipedia page.

Alon [A] showed that the list chromatic number of a graph (not necessarily bipartite) of maximum degree 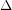$ \Delta $ is at least 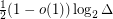$ \frac{1}{2}(1-o(1))\log_2\Delta $. Random bipartite graphs show that this is tight up to a multiplicative factor $ (2+o(1)) $.

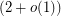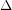It is not diffcult to see that the list chromatic number of any bipartite graph $ G $ of maximum degree $ \Delta $ is at most 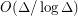$ O(\Delta/\log \Delta) $. It also follows a more general result of Johansson [J] on triangle-free graphs.

Bibliography

*[A] N. Alon, Degrees and choice numbers, Random Structures Algorithms, 16 (2000), 364--368.

[AK] N. Alon and M. Krivelevich, The choice number of random bipartite graphs, Annals of Combi- natorics 2 (1998), 291-297.

[J] A. Johansson. Asymptotic choice number for triangle free graphs. Technical Report 91–95, DIMACS, 1996.


* indicates original appearance(s) of problem.
add new comment