 login/create account
login/create account
Wood, David R.
Chromatic number of associahedron ★★
Author(s): Fabila-Monroy; Flores-Penaloza; Huemer; Hurtado; Urrutia; Wood
Conjecture Associahedra have unbounded chromatic number.
Geometric Hales-Jewett Theorem ★★
Conjecture For all integers 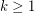 and
and 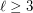 , there is an integer
, there is an integer 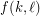 such that for every set
such that for every set  of at least
of at least 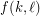 points in the plane, if each point in
points in the plane, if each point in  is assigned one of
is assigned one of  colours, then:
colours, then:
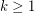 and
and 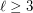 , there is an integer
, there is an integer 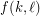 such that for every set
such that for every set  of at least
of at least 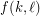 points in the plane, if each point in
points in the plane, if each point in  is assigned one of
is assigned one of  colours, then:
colours, then:- \item
 contains
contains 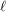 collinear points, or \item
collinear points, or \item  contains a monochromatic line (that is, a maximal set of collinear points receiving the same colour)
contains a monochromatic line (that is, a maximal set of collinear points receiving the same colour) Keywords: Hales-Jewett Theorem; ramsey theory
Generalised Empty Hexagon Conjecture ★★
Author(s): Wood
Conjecture For each 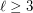 there is an integer
there is an integer 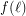 such that every set of at least
such that every set of at least 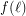 points in the plane contains
points in the plane contains 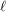 collinear points or an empty hexagon.
collinear points or an empty hexagon.
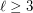 there is an integer
there is an integer 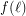 such that every set of at least
such that every set of at least 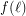 points in the plane contains
points in the plane contains 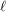 collinear points or an empty hexagon.
collinear points or an empty hexagon. Keywords: empty hexagon
Colouring $d$-degenerate graphs with large girth ★★
Author(s): Wood
Question Does there exist a  -degenerate graph with chromatic number
-degenerate graph with chromatic number 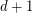 and girth
and girth  , for all
, for all 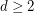 and
and 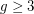 ?
?
 -degenerate graph with chromatic number
-degenerate graph with chromatic number 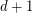 and girth
and girth  , for all
, for all 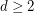 and
and 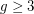 ?
? Keywords: degenerate; girth
Forcing a 2-regular minor ★★
Conjecture Every graph with average degree at least 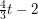 contains every 2-regular graph on
contains every 2-regular graph on  vertices as a minor.
vertices as a minor.
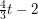 contains every 2-regular graph on
contains every 2-regular graph on  vertices as a minor.
vertices as a minor. Keywords: minors
Fractional Hadwiger ★★
Author(s): Harvey; Reed; Seymour; Wood
Conjecture For every graph  ,
,
(a)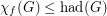
(b)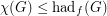
(c)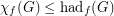 .
.
 ,
,(a)
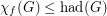
(b)
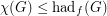
(c)
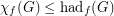 .
. Keywords: fractional coloring, minors
Forcing a $K_6$-minor ★★
Author(s): Barát ; Joret; Wood
Conjecture Every graph with minimum degree at least 7 contains a 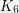 -minor.
-minor.
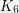 -minor.
-minor. Conjecture Every 7-connected graph contains a 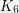 -minor.
-minor.
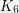 -minor.
-minor. Keywords: connectivity; graph minors
Point sets with no empty pentagon ★
Author(s): Wood
Problem Classify the point sets with no empty pentagon.
Keywords: combinatorial geometry; visibility graph
Number of Cliques in Minor-Closed Classes ★★
Author(s): Wood
Question Is there a constant  such that every
such that every  -vertex
-vertex 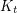 -minor-free graph has at most
-minor-free graph has at most 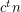 cliques?
cliques?
 such that every
such that every  -vertex
-vertex 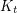 -minor-free graph has at most
-minor-free graph has at most 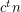 cliques?
cliques? Big Line or Big Clique in Planar Point Sets ★★
Let  be a set of points in the plane. Two points
be a set of points in the plane. Two points  and
and  in
in  are visible with respect to
are visible with respect to  if the line segment between
if the line segment between  and
and  contains no other point in
contains no other point in  .
.
Conjecture For all integers 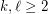 there is an integer
there is an integer  such that every set of at least
such that every set of at least  points in the plane contains at least
points in the plane contains at least 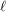 collinear points or
collinear points or  pairwise visible points.
pairwise visible points.
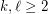 there is an integer
there is an integer  such that every set of at least
such that every set of at least  points in the plane contains at least
points in the plane contains at least 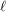 collinear points or
collinear points or  pairwise visible points.
pairwise visible points. Keywords: Discrete Geometry; Geometric Ramsey Theory

 Drupal
Drupal CSI of Charles University
CSI of Charles University