 login/create account
login/create account
 such that every
such that every  -vertex
-vertex 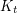 -minor-free graph has at most
-minor-free graph has at most 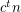 cliques?
cliques? Here a clique is a (not neccessarily maximal) set of pairwise adjacent vertices in a graph.
See [RW, NSTW] for early bounds on the number of cliques. Wood [W] proved that the number of cliques in an  -vertex
-vertex 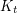 -minor-free graph is at most
-minor-free graph is at most 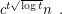 Fomin et al. [FOT] improved this bound to
Fomin et al. [FOT] improved this bound to 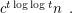
These results are based on the fact that every  -vertex
-vertex 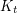 -minor-free graph has at most
-minor-free graph has at most 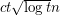 edges. This bound is tight for certain random graphs. So it is reasonable to expect that random graphs might also provide good lower bounds on the number of cliques.
edges. This bound is tight for certain random graphs. So it is reasonable to expect that random graphs might also provide good lower bounds on the number of cliques.
Update 2014: Choongbum Lee and Sang-il Oum [LO] recently answered this question in the affirmative, and even proved it for excluded subdivisions. In particular, they proved that every  -vertex graph with no
-vertex graph with no 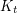 -subdivision has at most
-subdivision has at most 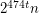 cliques and also at most
cliques and also at most 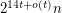 cliques.
cliques.
The question now is to determine the minimum constant. Wood [W] proved a lower bound of 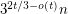 using an appropriate sized complete graph minus a perfect matching. The same graph gives a lower bound of
using an appropriate sized complete graph minus a perfect matching. The same graph gives a lower bound of 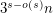 on the number of cliques in a graph with no
on the number of cliques in a graph with no 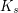 subdivision.
subdivision.
Update (2019): Fox and Wei [FW] have proved that every graph on  vertices with no
vertices with no 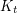 -minor has at most
-minor has at most 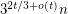 cliques. This bound is tight for
cliques. This bound is tight for 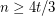 .
.
Bibliography
[FOT] Fedor V. Fomin, Sang il Oum, and Dimitrios M. Thilikos. Rank-width and tree-width of  -minor-free graphs, European J. Combin. 31 (7), 1617–1628, 2010.
-minor-free graphs, European J. Combin. 31 (7), 1617–1628, 2010.
[NSTW] Serguei Norine, Paul Seymour, Robin Thomas, Paul Wollan. Proper minor-closed families are small. J. Combin. Theory Ser. B, 96(5):754--757, 2006.
[RW] Bruce Reed and David R. Wood. Fast separation in a graph with an excluded minor. In 2005 European Conf. on Combinatorics, Graph Theory and Applications (EuroComb '05), vol. AE of Discrete Math. Theor. Comput. Sci. Proceedings, pp. 45--50. 2005.
* [W] David R. Wood. On the maximum number of cliques in a graph. Graphs Combin., 23(3):337--352, 2007.
[LO] Choongbum Lee and Sang-il Oum. Number of cliques in graphs with forbidden minor, 2014.
[FW] Jacob Fox, Fan Wei. On the number of cliques in graphs with a forbidden minor
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University