Home » Subject » Geometry

Chromatic number of associahedron

Importance: Medium ✭✭
Author(s): Fabila-Monroy, Ruy
Flores-Penaloza, David
Huemer, Clemens
Hurtado, Ferran
Urrutia, Jorge
Wood, David R.
Subject: Geometry
Keywords: associahedron, graph colouring, chromatic number
Recomm. for undergrads: yes
Posted by: David Wood
on: June 2nd, 2015
Conjecture   Associahedra have unbounded chromatic number.

An associahedron is the convex polytope in which each vertex corresponds to a way of correctly inserting opening and closing parentheses in a fixed word and the edges correspond to single application of the associativity rule. Equivalently, the vertices of an associahedron correspond to the triangulations of a convex polygon and the edges correspond to edge flips in which a single diagonal is removed from a triangulation and replaced by a different diagonal.

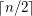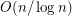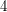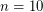The chromatic number of (the 1-skeleton of) associahedra was first considered by Fabila-Monroy et al [FFHHUW]. They proved that for the associahedron corresponding to edge flips in triangulations of a convex $ n $-gon, the chromatic number is at most $ \ceil{n/2} $ and at most $ O(n/\log n) $. The best known lower bound is $ 4 $ for $ n=10 $ [private communication, Ruy Fabila-Monroy].

Update (2019): Addario Berry et al. [ARSW] proved an upper bound of 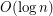$ O(\log n) $.

Bibliography

*[FFHHUW] Ruy Fabila-Monroy, David Flores-Penaloza, Clemens Huemer, Ferran Hurtado, Jorge Urrutia, David R. Wood. On the Chromatic Number of some Flip Graphs, Discrete Mathematics and Theoretical Computer Science Vol 11, No 2 (2009).

[ARSW] Louigi Addario Berry, Bruce Reed, Alex Scott, David R. Wood. A logarithmic bound for the chromatic number of the associahedron, 2018.


* indicates original appearance(s) of problem.
add new comment