 login/create account
login/create account
degenerate
Colouring $d$-degenerate graphs with large girth ★★
Author(s): Wood
Question Does there exist a  -degenerate graph with chromatic number
-degenerate graph with chromatic number 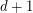 and girth
and girth  , for all
, for all 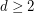 and
and 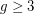 ?
?
 -degenerate graph with chromatic number
-degenerate graph with chromatic number 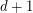 and girth
and girth  , for all
, for all 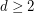 and
and 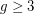 ?
? Keywords: degenerate; girth
Degenerate colorings of planar graphs ★★★
Author(s): Borodin
A graph  is
is  -degenerate if every subgraph of
-degenerate if every subgraph of  has a vertex of degree
has a vertex of degree 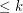 .
.
Conjecture Every simple planar graph has a 5-coloring so that for 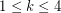 , the union of any
, the union of any  color classes induces a
color classes induces a 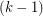 -degenerate graph.
-degenerate graph.
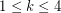 , the union of any
, the union of any  color classes induces a
color classes induces a 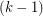 -degenerate graph.
-degenerate graph. Keywords: coloring; degenerate; planar

 Drupal
Drupal CSI of Charles University
CSI of Charles University