Home » Subject » Geometry

Geometric Hales-Jewett Theorem (Solved)

Importance: Medium ✭✭
Author(s): Por, Attila
Wood, David R.
Subject: Geometry
Keywords: Hales-Jewett Theorem
ramsey theory
Recomm. for undergrads: no
Posted by: David Wood
on: March 26th, 2014
Solved by: Vytautas Gruslys. "A counterexample to a geometric Hales-Jewett type conjecture", J. Computational Geometry, 5.1:245-249, 2014.
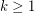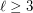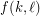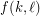Conjecture   For all integers $ k\geq1 $ and $ \ell\geq3 $, there is an integer $ f(k,\ell) $ such that for every set $ P $ of at least $ f(k,\ell) $ points in the plane, if each point in $ P $ is assigned one of $ k $ colours, then:
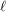    \item $ P $ contains $ \ell $ collinear points, or \item $ P $ contains a monochromatic line (that is, a maximal set of collinear points receiving the same colour)

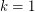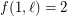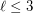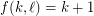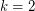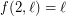This conjecture is trivially true for $ k=1 $ with $ f(1,\ell)=2 $, and for $ \ell\leq3 $ and $ f(k,\ell)=k+1 $. The Motzkin-Rabin Theorem [PS] says that the conjecture is true for $ k=2 $ with $ f(2,\ell)=\ell $. The conjecture is related to the Hales-Jewett Theorem, which states that for sufficiently large 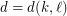$ d=d(k,\ell) $, every $ k $-colouring of the $ d $-dimensional grid 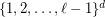$ \{1,2,\dots,\ell-1\}^d $ contains a monochromatic "combinatorial"' line of 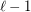$ \ell-1 $ points. Say the Geometric Hales-Jewett Theorem is the statement obtained by replacing "combinatorial line" by "geometric line" (that is, a set of collinear points). This theorem is discussed in [P]. The conjecture is a generalisation of the Geometric Hales-Jewett Theorem.

This conjecture was disproved by Vytautas Gruslys [G].

Bibliography

[P] D.H.J. Polymath. Density Hales-Jewett and Moser numbers, arXiv:1002.0374, 2010.

*[PW] Attila Pór and David R. Wood. On visibility and blockers, J. Computational Geometry 1:29-40, 2010.

[PS] Lou M. Pretorius and Konrad J. Swanepoel. An Algorithmic Proof of the Motzkin-Rabin Theorem on Monochrome Lines, The American Mathematical Monthly 111.3:245-251, 2004.

[G] Vytautas Gruslys. A counterexample to a geometric Hales-Jewett type conjecture. J. Comput. Geom. 5.1:245-249, 2014.


* indicates original appearance(s) of problem.
add new comment