 login/create account
login/create account
Seymour's Second Neighbourhood Conjecture
By the  th outdegree of
th outdegree of  , we mean the number of vertices for which the minimal outward-directed path from
, we mean the number of vertices for which the minimal outward-directed path from  to them is of length
to them is of length  .
.
Chen, Shen, and Yuster [CSY] proved that in any oriented graph there is a vertex whose second outdegree is at least 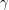 times its outdegree, where
times its outdegree, where 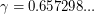 is the unique real root of
is the unique real root of 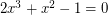 .
.
This conjecture implies a special case of the \Oprefnum[Caccetta-Häggkvist Conjecture]{46385}.
Bibliography
[ASY] Chen, G.; Shen, J.; Yuster, R. Second neighborhood via first neighborhood in digraphs, Annals of Combinatorics, 7 (2003), 15--20.
[F] Fisher, David C. Squaring a tournament: a proof of Dean's conjecture. J. Graph Theory 23 (1996), no. 1, 43--48.
[KL] Kaneko, Yoshihiro; Locke, Stephen C. The minimum degree approach for Paul Seymour's distance 2 conjecture. Proceedings of the Thirty-second Southeastern International Conference on Combinatorics, Graph Theory and Computing (Baton Rouge, LA, 2001). Congr. Numer. 148 (2001), 201--206.
* indicates original appearance(s) of problem.
Re: It is proved
Thanks for the reference. The proof, however, seems flawed. The basic outline of the proof (if I understood it correctly) is as follows:
- \item If
 has a sink, then this sink satisfies the conditions. \item An oriented graph without directed cycles has a sink. \item Then one proves directly that a graph containing a directed cycle has a vertex (even on that cycle) that satisfies the conditions.
has a sink, then this sink satisfies the conditions. \item An oriented graph without directed cycles has a sink. \item Then one proves directly that a graph containing a directed cycle has a vertex (even on that cycle) that satisfies the conditions. The last part (Lemma 2 of the manuscript), is not true -- take a directed cycle  , add many independent points
, add many independent points 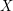 , and add all the arcs from
, and add all the arcs from  to
to 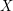 . Now the conjecture is true for this graph (one can take any of the sinks -- vertices in
. Now the conjecture is true for this graph (one can take any of the sinks -- vertices in 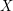 ), but it is not true that one can choose a vertex of
), but it is not true that one can choose a vertex of  .
.
The omission in the proof of Lemma 2 is that it's tacitly assumed, that adjacent vertices of the cycle have no common out-neighbours.
So is this proof valid or
So is this proof valid or not? I am currently working on a proof and am wondering whether or not I should be bothering
Re: So is this proof valid or
I believe the mentioned prof is not valid. Is your proof working? And sorry for the late reply, our system falsely recognized your comment as a spam.
Counterexample for the proof
As was indicated, Lemma 2 is false. Here is a counterexample to lemma 2. Note that it is not a counterexample to the conjecture, since it has two sinks.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
It is proved
This conjecture has been proved. You can find the proof here .