login/create account
Conjecture Any oriented graph has a vertex whose outdegree is at most its second outdegree.
By the 
th outdegree of 
, we mean the number of vertices for which the minimal outward-directed path from to them is of length .
Chen, Shen, and Yuster [CSY] proved that in any oriented graph there is a vertex whose second outdegree is at least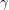 
times its outdegree, where 
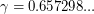is the unique real root of 
.
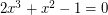This conjecture implies a special case of the \Oprefnum[Caccetta-Häggkvist Conjecture]{46385}.
Bibliography
[ASY] Chen, G.; Shen, J.; Yuster, R. Second neighborhood via first neighborhood in digraphs, Annals of Combinatorics, 7 (2003), 15--20.
[F] Fisher, David C. Squaring a tournament: a proof of Dean's conjecture. J. Graph Theory 23 (1996), no. 1, 43--48.
[KL] Kaneko, Yoshihiro; Locke, Stephen C. The minimum degree approach for Paul Seymour's distance 2 conjecture. Proceedings of the Thirty-second Southeastern International Conference on Combinatorics, Graph Theory and Computing (Baton Rouge, LA, 2001). Congr. Numer. 148 (2001), 201--206.
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University