Thanks for the reference. The proof, however, seems flawed. The basic outline of the proof (if I understood it correctly) is as follows:
\item If has a sink, then this sink satisfies the conditions. \item An oriented graph without directed cycles has a sink. \item Then one proves directly that a graph containing a directed cycle has a vertex (even on that cycle) that satisfies the conditions.
The last part (Lemma 2 of the manuscript), is not true -- take a directed cycle , add many independent points , and add all the arcs from to . Now the conjecture is true for this graph (one can take any of the sinks -- vertices in ), but it is not true that one can choose a vertex of .
The omission in the proof of Lemma 2 is that it's tacitly assumed, that adjacent vertices of the cycle have no common out-neighbours.
Re: It is proved
Thanks for the reference. The proof, however, seems flawed. The basic outline of the proof (if I understood it correctly) is as follows:
\item If has a sink, then this sink satisfies the conditions. \item An oriented graph without directed cycles has a sink. \item Then one proves directly that a graph containing a directed cycle has a vertex (even on that cycle) that satisfies the conditions.
has a sink, then this sink satisfies the conditions. \item An oriented graph without directed cycles has a sink. \item Then one proves directly that a graph containing a directed cycle has a vertex (even on that cycle) that satisfies the conditions.
The last part (Lemma 2 of the manuscript), is not true -- take a directed cycle , add many independent points
, add many independent points 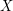 , and add all the arcs from
, and add all the arcs from  to
to 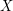 . Now the conjecture is true for this graph (one can take any of the sinks -- vertices in
. Now the conjecture is true for this graph (one can take any of the sinks -- vertices in 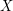 ), but it is not true that one can choose a vertex of
), but it is not true that one can choose a vertex of  .
.
The omission in the proof of Lemma 2 is that it's tacitly assumed, that adjacent vertices of the cycle have no common out-neighbours.