login/create account
Seymour's self-minor conjecture
Conjecture Every infinite graph is a proper minor of itself.
Robertson and Seymour famously proved that the set of all finite graphs is well-quasi-ordered by the minor relation. More precisely, if we let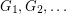 
be an infinite sequence of graphs, then there exist 
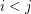so that 
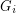is a minor of 
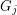. Their theory also gives us a rough structure theorem for the family of graphs without a fixed minor - a powerful tool for studying minors in finite graphs.
On the other hand, there are still large gaps in our understanding of minors of infinite graphs. For instance, while it is known that Wagner's conjecture does not hold in general for infinite graphs [T], it is possible that countably infinite graphs are well quasi-ordered.
The conjecture highlighted above is especially interesting, because (if true) it would imply the well quasi-ordering of finite graphs. Indeed, the well quasi-ordering of finite graphs is equivalent to the statement that every infinite set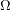 
of finite graphs contains two distinct members, one of which is a minor of the other. This latter statement follows from the above conjecture, since we may form a single infinite graph 
from the disjoint union of the graphs in 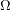, and the proper self-minor of gives us a pair of graphs in 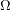with one a minor of the other.
Bibliography
[T] R. Thomas, A counterexample to "Wagner's conjecture" for infinite graphs. Math. Proc. Cambridge Philos. Soc. 103 (1988), no. 1, 55--57. MathSciNet
* indicates original appearance(s) of problem.
Real Problem
On April 15th, 2010 Anonymous says:
The real problem, of course, is to prove Seymour's Conjectre for countable graphs (which suffices for the Graph Minor Theorem). Note that Oporowski's example involves uncountable many vertices.
Drupal
CSI of Charles University
Counterexample to Seymour's self-minor conjecture
This conjecture has been shown to be false:
B. Oporowski, 'A counterexample to Seymour's self-minor conjecture.' Journal of Graph Theory, (14) 5 (521--524)