Home » Subject » Graph Theory » Infinite Graphs

Universal highly arc transitive digraphs

Importance: High ✭✭✭
Author(s): Cameron, Peter J.
Praeger, Cheryl E.
Wormald, Nicholas C.
Subject: Graph Theory
» Infinite Graphs
Keywords: arc transitive
digraph
Recomm. for undergrads: no
Posted by: mdevos
on: October 21st, 2007

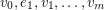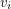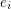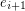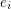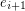An alternating walk in a digraph is a walk $ v_0,e_1,v_1,\ldots,v_m $ so that the vertex $ v_i $ is either the head of both $ e_i $ and $ e_{i+1} $ or the tail of both $ e_i $ and $ e_{i+1} $ for every 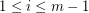$ 1 \le i \le m-1 $. A digraph is universal if for every pair of edges 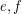$ e,f $, there is an alternating walk containing both $ e $ and $ f $

Question   Does there exist a locally finite highly arc transitive digraph which is universal?

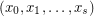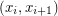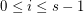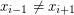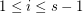Let $ D $ be a digraph. For a nonnegative integer $ s $, a $ s $-arc in $ D $ is a sequence $ (x_0,x_1,\ldots,x_s) $ of vertices so that $ (x_i,x_{i+1}) $ is an edge for every $ 0 \le i \le s-1 $ and $ x_{i-1} \neq x_{i+1} $ for every $ 1 \le i \le s-1 $. We say that $ D $ is $ s $-arc transitive if its automorphism group acts transitively on the set of $ s $ arcs, and we say that $ D $ is highly arc transitive if it is $ s $-arc transitive for every $ s $. Note that the condition $ 0 $-arc transitive is precisely equivalent to vertex transitive.

It is an easy exercise to show that the only finite digraphs which are highly arc transitive are directed cycles. Since such graphs have only trivial alternating walks (only one edge can be used), they are not universal. Thus, any graph satisfying the criteria of the conjecture must be infinite.

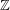Let $ P $ be a two way infinite directed path (i.e. the Cayley graph on $ {\mathbb Z} $ with generating set 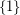$ \{1\} $). The digraph $ P $ is not universal, but moreover, any digraph with a homomorphism onto $ P $ cannot be universal. In the same article where the above question was posed, the authors asked wether there exist infinite highly transitive digraphs with no homomorphism onto $ P $. This question has since been resolved in the affirmative: Evans [E] constructed such a digraph with infinite indegree, and Malnic et. al. [MMSZ] have constructed a locally finite one.

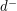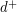In a vertex transitive digraph, every vertex must have the same indegree and the same outdegree, and we shall denote these by $ d^- $ and $ d^+ $ respectively. A theorem of Praeger [P] shows that every locally finite highly transitive digraph for which 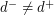$ d^- \neq d^+ $ has a homomorphism onto $ P $ and thus is not universal. More recently, Malnic et. al. 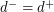[MMMSTZ] have established a condition on edge stabilizers in arc transitive digraphs which implies that any such digraph with $ d^- = d^+ $ a prime is not universal. It follows that any digraph satisfying the conditions of the highlighted question must have 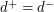$ d^+ = d^- $ a composite number.

Bibliography

*[CPW] P. J. Cameron, C. E. Praeger, and N. C. Wormald, Infinite highly arc transitive digraphs and universal covering digraphs. Combinatorica 13 (1993), no. 4, 377--396. MathSciNet.

[E] D. M. Evans, An infinite highly arc-transitive digraph, European J. Combin., 18 (1997) 281--286. MathSciNet.

[MMMSTZ] A. Malnic, D. Marusic, R. G. Moller, N. Seifter, V. Trofimov, and B. Zgrablic, Highly arc transitive digraphs: reachability, topological groups. European J. Combin. 26 (2005), no. 1, 19--28. MathSciNet.

[MMSZ] A. Malnic, D. Marusic, N. Seifter, and B. Zgrablic, Highly arc-transitive digraphs with no homomorphism onto Z. Combinatorica 22 (2002), no. 3, 435--443. MathSciNet

[P] C. E. Praeger, On homomorphic images of edge transitive directed graphs, Australas. J. Combin., 3 (1991), 207--210. MathSciNet.


* indicates original appearance(s) of problem.
add new comment