 login/create account
login/create account
Partitioning edge-connectivity
 be an
be an 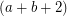 -edge-connected graph. Does there exist a partition
-edge-connected graph. Does there exist a partition 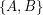 of
of 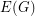 so that
so that 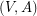 is
is  -edge-connected and
-edge-connected and 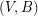 is
is  -edge-connected?
-edge-connected? By the Nash-Williams/Tutte theorem ([NW] or [T]) on disjoint spanning trees, the above conjecture is true if  is
is 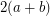 -edge-connected. This is the only partial result I know of. Here is a related conjecture.
-edge-connected. This is the only partial result I know of. Here is a related conjecture.
 so that every
so that every  -edge-connected graph
-edge-connected graph 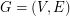 has a subset of edges
has a subset of edges  with the property that every edge-cut of
with the property that every edge-cut of  has between
has between 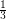 and
and 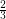 of its edges in
of its edges in  .
. The values 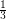 and
and 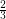 are of no special importance in the above conjecture. Indeed, an affirmative answer to the above problem with
are of no special importance in the above conjecture. Indeed, an affirmative answer to the above problem with 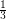 and
and 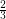 replaced by
replaced by 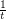 and
and 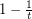 for any
for any 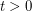 would still be valuable - and in particular, would imply the 2+epsilon flow conjecture.
would still be valuable - and in particular, would imply the 2+epsilon flow conjecture.
Definition: Let 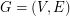 be a graph and let
be a graph and let 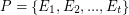 be a partition of
be a partition of  . We say that
. We say that  is
is  -courteous if
-courteous if 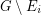 is
is  -edge-connected for every
-edge-connected for every 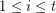 .
.
 so that every 3-edge-connected graph has a 2-courteous coloring of size
so that every 3-edge-connected graph has a 2-courteous coloring of size  ?
? It is known (see [DJS]) that 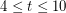 . It would be quite interesting if the truth were in fact
. It would be quite interesting if the truth were in fact 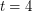 . An improvement on the current upper bound would have some consequences for certain flow problems and cycle-cover problems. In general, one may define a function
. An improvement on the current upper bound would have some consequences for certain flow problems and cycle-cover problems. In general, one may define a function 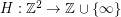 so that
so that 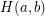 is the smallest integer
is the smallest integer  (or
(or 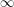 if none exists) so that every
if none exists) so that every  -edge-connected graph has a
-edge-connected graph has a  -courteous coloring of size
-courteous coloring of size  . It is known (see [DJS]) that
. It is known (see [DJS]) that 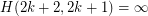 , and that
, and that 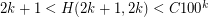 . Two special cases when better values are known are
. Two special cases when better values are known are 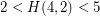 and
and 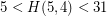 .
.
Bibliography
[DJS] M. DeVos, T. Johnson, P.D. Seymour, Cut-coloring and circuit covering
[Ed] J. Edmonds, Minimum Partition of a Matriod into Independent Subsets, J. Res. Nat. Bur. Standards 69B (1965) 67-72. MathSciNet
[NW] C.S.J.A. Nash-Williams, Edge Disjoint Spanning Trees of Finite Graphs, J. London Math. Soc. 36 (1961) 445-450. MathSciNet
[T] W.T. Tutte, On the problem of decomposing a graph into n connected factors, J. London Math. Soc. 36 (1961), 221-230. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University