 login/create account
login/create account
Weak pentagon problem
 is a cubic graph not containing a triangle, then it is possible to color the edges of
is a cubic graph not containing a triangle, then it is possible to color the edges of  by five colors, so that the complement of every color class is a bipartite graph.
by five colors, so that the complement of every color class is a bipartite graph. This conjecture has several reformulations: the conclusion of the conjecture can be replaced by either of the following:
- \item
 has a homomorphism to the Clebsch graph. \item there is a cut-continuous mapping from
has a homomorphism to the Clebsch graph. \item there is a cut-continuous mapping from  to
to 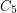 .
. For the latter variant, few definitions are in place. A cut-continuous mapping from a graph~ to a graph~
to a graph~ is a mapping
is a mapping 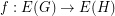 such that the preimage of every cut in~
such that the preimage of every cut in~ is a cut in~
is a cut in~ . Here, by a cut in~
. Here, by a cut in~ we mean the edge-set of a spanning bipartite subgraph of~
we mean the edge-set of a spanning bipartite subgraph of~ ---less succinctly, it is the set of all edges leaving some subset of vertices of~
---less succinctly, it is the set of all edges leaving some subset of vertices of~ .
.
Cut-continuous mappings are closely related with graph homomorphisms (see [DNR], [S]). In particular, every homomorphism from~ to~
to~ naturally induces a cut-continuous mapping from~
naturally induces a cut-continuous mapping from~ to~
to~ ; thus, the presented conjecture can be thought of as a weaker version of Nesetril's Pentagon problem.
; thus, the presented conjecture can be thought of as a weaker version of Nesetril's Pentagon problem.
We mention a generalization of the conjecture, that deals with longer cycles/larger number of colors. The  -dimensional projective cube, denoted
-dimensional projective cube, denoted 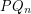 , is the simple graph obtained from the
, is the simple graph obtained from the 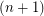 -dimensional cube~
-dimensional cube~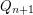 by identifying pairs of antipodal vertices (vertices that differ in all coordinates). Note that
by identifying pairs of antipodal vertices (vertices that differ in all coordinates). Note that 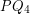 is the Clebsch graph.
is the Clebsch graph.
 with the property that all cubic graphs of sufficiently high girth have a homomorphism to
with the property that all cubic graphs of sufficiently high girth have a homomorphism to 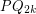 ?
? Again, the question has several reformulations due to the following simple proposition.
 and nonnegative integer
and nonnegative integer  , the following properties are equivalent.
, the following properties are equivalent.- \item There exists a coloring of~
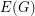 by
by 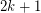 colors so that the complement of every color class is a bipartite graph. \item
colors so that the complement of every color class is a bipartite graph. \item  has a homomorphism to
has a homomorphism to 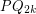 \item
\item  has a cut-continuous mapping to~
has a cut-continuous mapping to~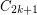
There are high-girth cubic graphs with the largest cut of size less then 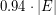 . Such graphs do not admit a homomorphism to
. Such graphs do not admit a homomorphism to 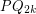 for any
for any 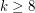 , so there is indeed some largest integer~
, so there is indeed some largest integer~ in the above question. To bound this largest~
in the above question. To bound this largest~ from below, recall that every cubic graph maps homomorphically to
from below, recall that every cubic graph maps homomorphically to 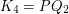 . Moreover, it is known [DS] that cubic graphs of girth at least 17 admit a homomorphism to
. Moreover, it is known [DS] that cubic graphs of girth at least 17 admit a homomorphism to 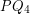 (the Clebsch graph). This shows
(the Clebsch graph). This shows 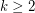 (and also provides a support for the main conjecture).
(and also provides a support for the main conjecture).
Bibliography
[DNR] Matt DeVos, Jaroslav Nesetril and Andre Raspaud: On edge-maps whose inverse preserves flows and tensions, \MRref{MR2279171}
*[DS] Matt Devos, Robert Samal: \arXiv[High Girth Cubic Graphs Map to the Clebsch Graph}{math.CO/0602580}
[S] Robert Samal, On XY mappings, PhD thesis, Charles University 2006, tech. report
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University