 login/create account
login/create account
Conjecture Suppose that  is a
is a  -edge-critical graph. Suppose that for each edge
-edge-critical graph. Suppose that for each edge  of
of  , there is a list
, there is a list 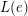 of
of  colors. Then
colors. Then  is
is  -edge-colorable unless all lists are equal to each other.
-edge-colorable unless all lists are equal to each other.
 is a
is a  -edge-critical graph. Suppose that for each edge
-edge-critical graph. Suppose that for each edge  of
of  , there is a list
, there is a list 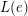 of
of  colors. Then
colors. Then  is
is  -edge-colorable unless all lists are equal to each other.
-edge-colorable unless all lists are equal to each other. (Reproduced from [M].)
A graph  is said to be
is said to be  -edge-critical if it is not
-edge-critical if it is not  -edge-colorable but every edge-deleted subgraph is
-edge-colorable but every edge-deleted subgraph is  -edge-colorable. (Here
-edge-colorable. (Here  is the maximum degree of
is the maximum degree of  .)
.)
Bibliography
*[M] B. Mohar, Problem of the Month
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University