 login/create account
login/create account
Conjecture Let 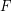 is a family of multifuncoids such that each
is a family of multifuncoids such that each 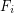 is of the form
is of the form 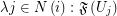 where
where 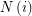 is an index set for every
is an index set for every 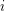 and
and 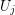 is a set for every
is a set for every 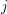 . Let every
. Let every 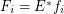 for some multifuncoid
for some multifuncoid 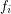 of the form
of the form 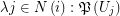 regarding the filtrator
regarding the filtrator 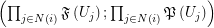 . Let
. Let  is a graph-composition of
is a graph-composition of 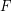 (regarding some partition
(regarding some partition  and external set
and external set 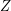 ). Then there exist a multifuncoid
). Then there exist a multifuncoid 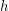 of the form
of the form 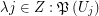 such that
such that 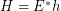 regarding the filtrator
regarding the filtrator 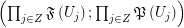 .
.
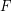 is a family of multifuncoids such that each
is a family of multifuncoids such that each 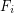 is of the form
is of the form 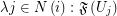 where
where 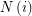 is an index set for every
is an index set for every 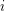 and
and 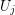 is a set for every
is a set for every 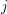 . Let every
. Let every 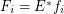 for some multifuncoid
for some multifuncoid 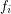 of the form
of the form 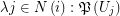 regarding the filtrator
regarding the filtrator 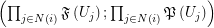 . Let
. Let  is a graph-composition of
is a graph-composition of 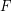 (regarding some partition
(regarding some partition  and external set
and external set 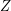 ). Then there exist a multifuncoid
). Then there exist a multifuncoid 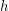 of the form
of the form 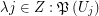 such that
such that 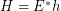 regarding the filtrator
regarding the filtrator 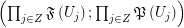 .
. See Algebraic General Topology, especially the theory of multifuncoids for definitions of used concepts.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University