 login/create account
login/create account
multifuncoid
Several ways to apply a (multivalued) multiargument function to a family of filters ★★★
Author(s): Porton
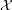 be an indexed family of filters on sets. Which of the below items are always pairwise equal?
be an indexed family of filters on sets. Which of the below items are always pairwise equal?
1. The funcoid corresponding to this function (considered as a single argument function on indexed families) applied to the reloidal product of filters 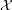 .
.
2. The funcoid corresponding to this function (considered as a single argument function on indexed families) applied to the starred reloidal product of filters 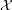 .
.
3. 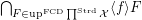 .
.
Keywords: funcoid; function; multifuncoid; staroid
Graph product of multifuncoids ★★
Author(s): Porton
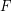 is a family of multifuncoids such that each
is a family of multifuncoids such that each 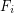 is of the form
is of the form 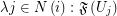 where
where 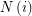 is an index set for every
is an index set for every 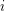 and
and 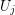 is a set for every
is a set for every 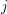 . Let every
. Let every 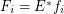 for some multifuncoid
for some multifuncoid 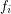 of the form
of the form 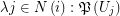 regarding the filtrator
regarding the filtrator 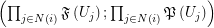 . Let
. Let  is a graph-composition of
is a graph-composition of 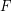 (regarding some partition
(regarding some partition  and external set
and external set 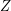 ). Then there exist a multifuncoid
). Then there exist a multifuncoid 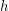 of the form
of the form 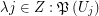 such that
such that 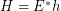 regarding the filtrator
regarding the filtrator 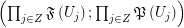 .
. Keywords: graph-product; multifuncoid
Atomicity of the poset of multifuncoids ★★
Author(s): Porton
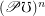 is for every sets
is for every sets 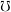 and
and  :
:- \item atomic; \item atomistic.
See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords: multifuncoid
Atomicity of the poset of completary multifuncoids ★★
Author(s): Porton
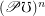 is for every sets
is for every sets 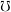 and
and  :
:- \item atomic; \item atomistic.
See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords: multifuncoid

 Drupal
Drupal CSI of Charles University
CSI of Charles University